A kind of grid is sometimes used for encoding messages. Our naval fleet officials decide to use this kind of encoding messages for communication with their ship captains. The encoding grid is a square sheet of paper divided into 2N x 2N little squares. N2 of little squares are cut out (see figure 1).
Let us briefly describe the encoding process. Take text of message of length 4N2. Then put an encoding grid onto a blank sheet of paper and begin to write first N2 letters of message into the cut little squares (one letter per square, write letters in all cut squares in the first line from left to right, then in the second line etc.). See example on figure 2 for message "HELLOYELLOWWORLD". After finishing the first step rotate the encoding grid 90 degrees clockwise and continue similarly writing letters. After two more steps all letters should be written (see example on figure 3).
O### H### HOOY ##O# ##E# LREO O##O L##L LWEL #### #### LLDW (fig. 1) (fig. 2) (fig. 3)It is necessary to have a correctly constructed grid. It means that when it is used in the way described above after each rotation new N2 blank squares will appear under cut squares of the grid.
The naval fleet officials encoded thousands of messages with their grid and then they wanted to send them to ships. Unfortunately they lost the grid. Fortunately the naval admiral remembered the original text of one of the messages.
Your task is to get this original message text and encoded text and find one possible correctly constructed encoding grid with which the message text could have been encoded.
Input Data
The first line of input file contains an integer N (1<=N<=10). The second line contains 4N2 capital letters representing the original message. The next 2N lines contain the encoded text (each line 2N capital letters).
Output Data
The output file contains a correctly constructed grid with which given message could have been encoded. In each of 2N lines one line of grid (2N characters) will be displayed where "O" (capital letter 'O' represents cut square and "#" uncut square).
Example
GRID.IN
2 HELLOYELLOWWORLD HOOY LREO LWEL LLDWGRID.OUT
O### ##O# O##O ####
The Palmia country is divided by a river into the north and south bank. There are N towns on both the north and south bank. Each town on the north bank has its unique friend town on the south bank. No two towns have the same friend.
Each pair of friend towns would like to have a ship line connecting them. They applied for permission to the government. Because it is often foggy on the river the government decided to prohibit intersection of ship lines (if two lines intersect there is a high probability of ship crash).
Your task is to write a program to help government officials decide to which ship lines they should grant permission to get maximum number of non intersecting ship lines.
Input Data
The input file consists of several blocks. In the first line of each there are 2 integers X,Y separated with exactly one space, X represents the length of the Palmia river bank (10 <= X <= 6000), Y represents the width of the river (10 <= Y <= 100). The second line contains the integer N, the number of towns situated on both south and north riverbanks (1 <= N <= 5000). On each of the next N lines there are two non-negative integers C,D separated with space (C,D <= X), representing distances of the pair of friend towns from the western border of Palmia measured along the riverbanks (C for the town on the north bank, D for the town on the south bank). There are no two towns on the same position on the same riverbank. After the last block there is a single line with two numbers 0 separated by a space.
Output Data
For each block of the input file the output file has to contain in consecutive lines the maximum possible number of ship lines satisfying the conditions above.
Example
SHIPS.IN
30 4 7 22 4 2 6 10 3 15 12 9 8 17 17 4 2 0 0SHIPS.OUT
4
In Palmia country they have N cities connected by highways (each highway connects exactly two cities in both directions). It is possible to reach every city from any other city using one or several highways. Till this year the highway tolls were collected on highways. In the middle of each highway there was a toll collector who collected 1 Palmia Coin (1 PC) from each car passing by.
Government officials decided to reduce the number of toll collectors and introduce highway stamps. If a car will want to enter a highway it must have this higway stamp placed on the window.
Officials decided that the highway stamp for one year will cost the same as 100 travels between two farthest cities. The distance between two cities is the minimum number of highways you need to use to get from the first city to the second one.
Your task is to write a program which computes the cost of the highway stamp.
Input Data
The input file consists of several blocks of data. Each block at the first line contains the integers N and M separated by a space where N is the number of cities and M the number of highways in Palmia country (1<= N <= 1000, 1 <= M <= 2000). Cities are numbered by integers from 1 to N. The next M lines contain each one pair of integers A,B (1<= A,B <= N) separated by a space representing that there is a highway between the cities A and B. After the last block there is a single line with two numbers 0 separated by a space.
Output Data
For each block of input file the output file contains a single line with the cost of the highway stamp.
Example
TOLLS.IN
4 4 1 2 2 3 4 2 3 4 0 0TOLLS.OUT
200
A factory has a bin packing robot at the end of an assembly line. There are exactly two bins open, and the robot packs items into any one of the open bins, one by one sequentially. The bins are identical, and one bin can accommodate a set of items up to a given weight limit. More precisely, the robot can perform the following four instructions:
Input Data
The input file contains integer numbers. The first line of input file contains the weight limit L (1 <= L <= 100). This limit applies to all bins. The second line contains the number of items N (1 <= N <=5000). Each of the following N lines contains the weight of an item. Each weight is at least 1 and at most L.
Output Data
Write on the first line of output file the minimum number of bins needed to pack all items.
Example
BINPACK.IN
8 6 4 2 5 3 5 4BINPACK.OUT
3
You are given a rectangle whose side lengths are integer numbers. You want to cut the rectangle into the smallest number of squares, whose side lengths are also integer numbers. Cutting can be performed with a cutting machine that can cut only from side to side across, parallel with one side of the rectangle. Obtained rectangles are cut separately.
Input Data
The input file contains two positive integers in the first line: the lengths of the sides of the rectangle. Each side of the rectangle is at least 1 and at most 100.
Output Data
The output file consist of one line on which your program should write the number of squares resulting from an optimal cutting.
Example
CUTS.IN
5 6CUTS.OUT
5
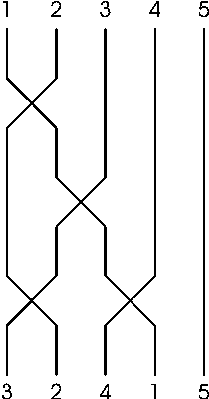
The electrician Fero has just finished the installation of the new cable in the building of the CEOI secretariat. The cable consists of N wires and connects the computer room and CEOI secretary office. In the computer room Fero labeled the wires with numbers from 1 to N from left to right. Because the cable was long, sometimes some of wires crossed between the computer room and the office (each pair of wires crosses at most once; at each moment only neighbouring wires may cross). So in the office the wires were not ordered the same way (see figure 1).
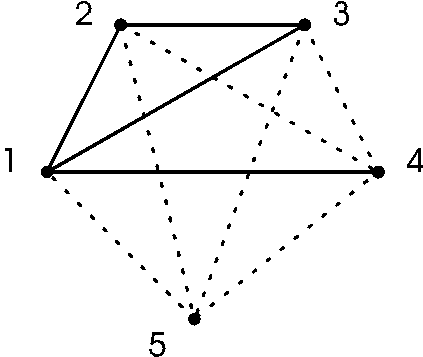
To know how these wires are crossed Fero drew the graph on the wall near the cable end in the computer room. The vertices represented wires and edges represented wire crosses. There is an edge between vertices a and b if and only if the wires a and b are crossed somewhere on the way (see figure 2 for graph representing situation in figure 1).
The cable does not function properly now. Unfortunately Fero broke his leg yesterday. We have another electrician but he is not so experienced in graph theory. He needs to know the order of wires at the end of the cable in the CEOI secretary office to correct this fault.


Input Data
In the input file there are several blocks of data. The first line of each block contains two numbers N and M separated by a space, where N (1<= N <= 100) is the number of wires in the cable and M is the number of wire crosses. This is followed by M lines each containing pair of integers A, B separated by a space (1 <= A,B <= N) representing the cross of cable wires A and B somewhere on the way. After the last block there is a line with two numbers 0.
Output Data
For each block of the input file the output file contains a single line with the list of wire numbers in order as they appear at the second end of the cable (N numbers separated by space) or the message "IMPOSSIBLE" if no order is represented by given graph.
Example
ELECTRIC.IN
5 4 1 2 1 3 2 3 1 4 0 0ELECTRIC.OUT
3 2 4 1 5