71. LAIPSNIAI.
|
|
|
|
|
|
|
1 50 | 01 | Paprastas atvejis |
|
|
1289 1 | 89 | Kitas paprastas atvejis |
|
|
123 3 | 67 63 47 23 | Testas, kuris buvo pateiktas sąlygoje |
|
|
12 3 | 28 52 08 12 | Keliant duotąjį skaičių laipsniu, nebus viršytas maxint |
|
|
1425 48 | 25 | Periodą sudaro tik vienas skaičius |
|
|
5872 2 | 56 36 96 16 | Periodas prasideda ne pirmąja rasta galūne |
|
|
9887 39 | 23 87 | Atsitiktinis testas |
72. PINIGAI PAŠTU.
|
|
|
|
|
|
|
7 3
2187 729 243 81 27 9 3 |
0 | Neiškrenta nė vienas žaidėjas |
|
|
6 5
5400 1178 275 55 11 3 |
693 | Atsitiktinis testas |
|
|
8 5
21008 5410 1241 1240 248 76 18 4 |
11945 | Atsitiktinis testas |
|
|
10 61 1 1 1 1 1 1 1 1 1 | 50 | Iškrito beveik visi žaidėjai |
73. LYGIAGRETŪS PROCESAI.
|
|
|
|
74. KORTŲ KALADĖS.
|
|
|
|
|
|
Kaladės identiškos |
|
|
|
Pirmoji kaladė nuo antrosios skiriasi tuo, kad sukeistos pirma ir paskutinė kortos |
|
|
|
Norint sutapatinti kalades, reiktų pirmąją kaladę keliant dalinti į tris dalis |
|
|
|
Pirmoji kaladė tai antroji kaladė, paslinkta per vieną kortą. |
|
|
|
Iš pirmosios galima gauti antrąją |
|
|
|
|
|
|
Negalima |
|
|
Buvo 14 stotelių, prisidėjo 2;
Buvo 29 stotelės, prisidėjo 1; |
|
|
Pradinis duomuo lygus dvejeto laipsniui |
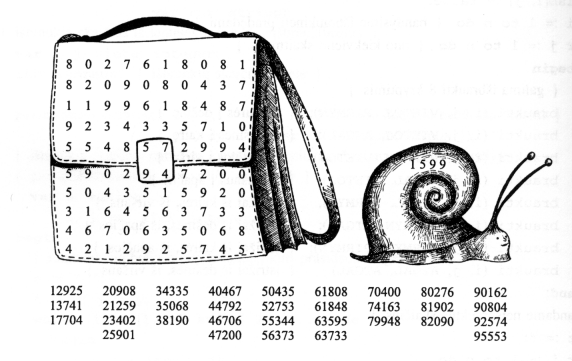
76. SKAIČIŲ BRAUKYMAS.
|
to nr. |
|
kiami skaičiai |
|
|
|
|
10
... |
32 5 | 1599 | Šis testas pavaizduotas žemiau esančiame pav. |
|
|
10
0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 |
6 5
10000 10100 10101 10111 11000 11010 |
00000 | Sutinkami tik du skaitmenys: 0 ir 1 |
|
|
10
|
17 3
|
9999999999 | Šis testas jau sudėtingesnis, yra 10 skirtingų skaitmenų; |
|
|
14
|
47 7
|
00001222344456788 | Sudėtingiausias testas;
kartu tikrinama, ar rezultatai surūšiuoti didėjimo tvarka. |

76.1 pav.
77. DAUG SKAIČIŲ.
|
nr. |
|
|
|
|
63
|
Visi skaičiai iš intervalo [1..62, 64..100] pateikti atsitiktine tvarka; skaičiai nesikartoja |
|
|
3001
|
Iš viso 15000 skaičių; pradiniai duomenys neviršija maxint, yra pasikartojančių skaičių |
|
|
70378
|
Iš viso 100000 skaičių; pradiniai duomenys viršija maxint, yra pasikartojančių skaičių |
|
|
456
|
Iš viso 200000 skaičių; pradiniai duomenys neviršija maxint, yra pasikartojančių skaičių |
|
nr. |
duomuo |
|
|
|
|
105 210 315 420 |
|
|
|
3003 6006 9009 12012 15015 |
|
|
|
15935205 31870410 47805615 63740820 79676025 95611230 111546435 |
79. PREKIŲ KONTEINERIAI.
|
|
Konteinerių skaičius |
Pelnas |
|
|
|
10
9 1000 1 100 5 600 7 700 7 800 3 400 3 300 1 200 9 900 |
5400
8 7 6 10 3 4 5 9 1 2 |
Kiekviename teste vis didėja pradinių duomenų kiekis; Tikrinama, ar laiko atžvilgiu sprendimas yra efektyvus; Pirmasis testas pateiktas visas, likusių tik testų matmenys ir rezultatuose gaunamas pelnas. |
|
|
500
... |
25491
... |
|
|
|
600
... |
29318
... |
|
|
|
1000
... |
25619
... |
80. NEPATIKIMAS RYŠYS.
A blankas
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B blankas
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C blankas
S procedūra
| S = proc (x?Praneš & st!ŽPraneš & as?Praneš). |
| begin m: var ŽPraneš & a: var Praneš |
| | m.ž := 0 ; x?m.p |
| ; while true |
| do st!m ; as?a |
| ; if a <> K |
| then if a <> m.ž |
| then m.ž := 1 - m.ž ; x?m.p |
| fi |
| fi |
| od |
| end |
| G = proc (tg?ŽPraneš & ga!Praneš & y?Praneš). |
| begin m: var ŽPraneš & u: var Nat |
| | u := 0 |
| ; while true |
| do tg?m |
| ; if m = K then ga!u |
| else if m.ž = u |
| then y!m.p ; u := 1 - u |
| fi |
| ; ga!u |
| fi |
| od |
| end |
81. GRAŽIOS LYGTYS.
|
|
|
|
|
|
|
2 4 | Gražių lygčių nėra | |
|
|
2 6 | 2 6 4 -1 -2 | 2x2 + 6x + 4 = 2(x + 1)(x + 2) |
|
|
-5 5 | 1 5 4 -1 -4
1 4 3 -1 -3 1 3 2 -1 -2 1 4 -5 1 -5 1 3 -4 1 -4 1 2 -3 1 -3 1 1 -2 1 -2 1 -1 -2 2 -1 1 -3 2 2 1 1 -2 -3 3 -1 1 -4 3 3 1 1 -3 -4 4 -1 1 -5 4 4 1 1 -4 -5 5 -1 |
x2 + 5x + 4 = (x + 1)(x + 4)
x2 + 4x + 3 = (x + 1)(x + 3) x2 + 3x + 2 = (x + 1)(x + 2) x2 + 4x - 5 = (x - 1)(x + 5) x2 + 3x - 4 = (x - 1)(x + 4) x2 + 2x - 3 = (x - 1)(x + 3) x2 + x - 2 = (x - 1)(x + 2) x2 - x - 2 = (x - 2)(x + 1) x2 - 3x + 2 = (x - 2)(x - 1) x2 - 2x - 3 = (x - 3)(x + 1) x2 - 4x + 3 = (x - 3)(x - 1) x2 - 3x - 4 = (x - 4)(x + 1) x2 - 5x + 4 = (x - 4)(x - 1) x2 - 4x - 5 = (x - 5)(x + 1) |
82. GRIOVELIAI.
|
|
|
mažiausio kvadrato dydis |
|
|
|
4 4 | 3
+++ III +OI |
nn > k; k = 3 |
|
|
99 0 | 99 | Nėra plokštelių su dviem grioveliais |
|
|
100 100 | 15 | nn > k; k = 15; plokštelės telpa į minimalų kvadratą |
|
|
100 6 | 16 | nn <= k; k = 11; plokštelės netelpa į minimalų kvadratą |
|
|
17 82 | 10 | nn <= k; k = 10; plokštelės telpa į minimalų kvadratą |
83. RUBIKO KUBAS.
|
|
(labirinto dydis, taškai A ir B, kliūčių skaičius) |
|
|
|
17, 1 5 3, 1 2 1, 8 |
7
|
|
|
29, 1 15 15, 29 15 15, 17 |
32
|
|
|
30, 1 1 1, 30 30 1, 16465 |
1032
|
84. DAUGIAKAMPIS.
|
|
|
|
|
|
2 400 0 0 | TAIP |
|
|
200 600 70 130 | TAIP |
|
|
0 0 166 40 | TAIP |
|
|
2 0 0 18 | TAIP |
|
|
0 188 56 0 | TAIP |
|
|
2 3 0 0 | NE |
|
|
121 20 71 50 | NE |
|
|
40 40 77 0 | NE |
|
|
0 0 0 144 | NE |
|
|
3 4 5 0 | NE |