Vienuoliktoji moksleivių informatikos olimpiada

Pirmojo etapo uždavinių testai

Jaunesniųjų grupė
173. NETIKRA MONETA. Monetas sunumeruojame nuo 1 iki 10. Netikros monetos ieškojimas pavaizduotas paveikslėlyje. Šis sprendimas nėra vienintelis. Iš jo matome, kad turint 10 monetų užteks trijų svėrimų.

174. VAIZDO ĮRAŠAI.

Pirmoje kiekvieno duomenų rinkinio eilutėje nurodytas laidų skaičius n, o likusiose n eilučių – kiekvienos laidos trukmė. Pirma nurodomas valandų, paskui minučių skaičius.
 
Testo nr.
1
2
3
4
5
6
7
8
9
10
11
Pradiniai duomenys
 1
1 10		 3
2 00
2 00
0 30		 4
0 30
0 20
3 40
1 30		 3
2 30
2 30
1 01		 5
1 10
1 05
1 00
4 45
1 00		 5
1 10
1 05
1 00
4 45
1 05		 3
5 30
3 20
2 00		 3
5 00
5 00
3 00		 3
5 00
5 00
3 05		 6
3 00
3 00
3 00
3 00
3 00
0 55		 6
8 30
8 30
8 30
8 30
8 30
2 00
Bendra laidų trukmė
1:10
4:30
6:00
6:01
9:00
9:05
10:50
13:00
13:05
15:55
44:30
Valandų skaičius
2
5 
 6 7 9 10 11 13 14 16 45
Ilgų ir trumpų vaizdajuosčių skaičius
 0 1 0 2 0 2 1 1 0 3 1 2 2 1 1 3 2 2 4 0 9 3
Rezultatas
 9,15 18,30 18,30 20,05 27,45 29,20 30,95 38,35 40,10 43,60 125,55

 
Testo nr.
Paaiškinimai
1
 Viena laida, telpa į vieną trumpą vaizdajuostę;
2
 Kelios laidos, telpa į dvi trumpas vaizdajuostes;
3
 Laidos užpildo dvi trumpas vaizdajuostes;
4
 Kelios laidos, telpa į trumpą ir ilgą vaizdajuostes (į dvi trumpas netilptų viena minutė);
5
 Laidos užpildo tris trumpas vaizdajuostes;
6
 Laidos telpa į  dvi trumpas ir vieną ilgą vaizdajuostę (į tris trumpas netilptų 5 minutės);
7
 Laidos telpa į vieną trumpą ir dvi ilgas vaizdajuostes;
8
 Laidos visiškai užpildo į tris trumpas ir vieną ilgą vaizdajuostę;
9
 Tas pats, kas 8 testas, tik 5 minutės nebetelpa, todėl rašoma į dvi trumpas ir dvi ilgas vaizdajuostes;
10
 Laidos visiškai užpildo keturias ilgas vaizdajuostes;
11
 Testas su didesne bendra laidų trukme;

175. KALADĖLIŲ DĖLIOJIMAS.
Testo nr.
Pradinis duomuo
Rezultatai
Paaiškinimai
1
 3 1 1 1 Kvadratai – atskiros plytelės
2
 35 25 9 1 Trys atsitiktinai parinkti didėjantys testai
3
 89 81 4 4
4
 149 144 4 1
5
 225 225 Pradinis duomuo yra kvadratas
6
 32767 32761 4 1 1 Maksimali pradinio duomens reikšmė

Pirmojo etapo uždavinių testai

Vyresniųjų grupė


















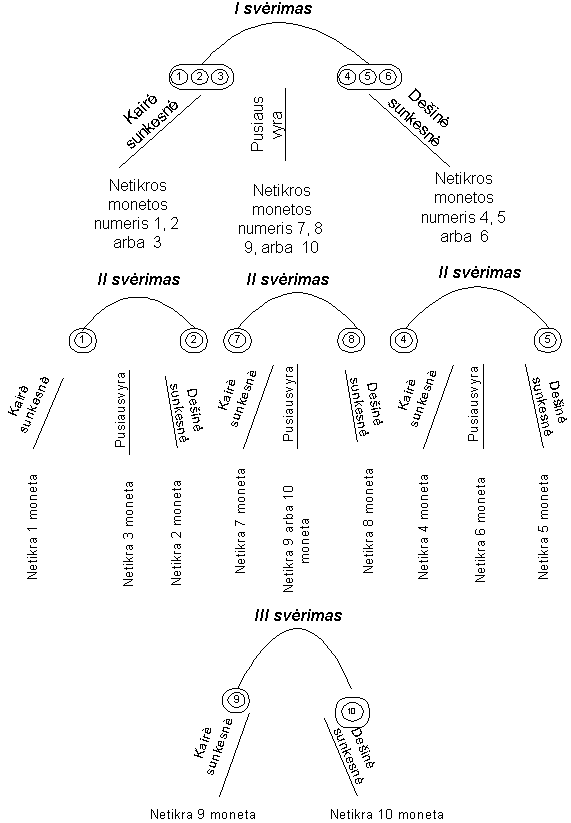
176.  NETIKRA MONETA.
a) Monetas sunumeruojame nuo 1 iki 10. Netikros monetos ieškojimas pavaizduotas paveikslėlyje. Šis sprendimas nėra vienintelis. Iš jo matome, kad turint 10 monetų užteks trijų ėjimų.

b)
Testo nr.
Pradinis duomuo
Rezultatas
Paaiškinimai
1
 2 1 Ribiniai atvejai (užtenka vieno svėrimo)
2
 3 1
3
 10 3 Sutampa su a) dalimi
4
 728 6 Keturiais testais tikrinama, ar teisingai randama riba kada padidėja svėrimų skaičius
5
 729 6
6
 730 7
7
 731 7
8
 32767 10 Ribinis atvejis – maksimalus monetų skaičius

177. GAUKITE SKAIČIŲ.
Testo nr.
Pradinis
duomuo
Rezultatai
Paaiškinimai
1
 857 NĖRA SPRENDINIO  Nėra sprendinio
2
 145 123 – 4 – 56 – 7 + 89
1 + 23 + 45 – 6 – 7 + 89
1 + 23 – 4 + 56 + 78 – 9
1 + 2 + 3 – 4 + 56 + 78 + 9		 Yra keli sprendiniai
3
 501 1234 + 56 – 789 Yra vienintelis sprendinys 
4
 -256 1 – 234 – 5 + 6 – 7 – 8 – 9
1 – 2 – 345 – 6 + 7 + 89		 Pradinis duomuo – neigiamas skaičius
5
 123456789 123456789 Tarp skaitmenų nereikia įterpti nė vieno ženklo















178. UŽRAŠAS SPIRALE.
Pradinių duomenų lentelė
Testo nr.
Pradiniai duomenys
Paaiškinimai
1
 Vakaras. Labai trumpas sakinys; jame nėra tarpų
2
 Olimpiada vyko tik gruodžio mėnesį. Trys atvejai, kuriais patikrinama, ar spiralė tikrai nėra pastumta nuo krašto
3
 Jo lėktuvas Frankfurte leidosi nevėluodamas.
4
 Londonas bus paskendęs tirštame rūke.
5
 Naujojo namo statyba dėl lėšų stokos jau keleri metai buvo sustojusi  Maksimalus simbolių skaičius sakinyje

Rezultatų lentelė
 
1
2
3
4
5
 .s
  a
V r
aka		 .įsenėm
      +
v+ada o
y   i i
k O p ž
o lim d
+     o
tik+gru		 ulėven+is 
o       o 
d savut d
a +   k i
m F J ė e 
a r o+l l 
s a     + 
. nkfurte		 .ekūr+ema
        t
  ub+sa š
  s   n r
  + L o i
  p ond t
  a     +
  skendęs		         .is
          u
+sokots+ų j
j       š o
a man+o ė t
u o   j l s
+ + N o + u
k s auj l s
e t     ė +
l atyba+d o
e         v
ri+metai+bu


Antrojo etapo uždavinių testai

Jaunesniųjų grupė

179. TREČIASIS TŪKSTANTMETIS.
Norint ištestuoti sprendimą, reikėtų turėti uždavinį sprendžiančią programą (ją galite rasti prie šios olimpiados šio etapo sprendimų) arba pagal kompiuterio rodomą laiką popieriuje apskaičiuoti likusių dienų, valandų bei minučių skaičių.

Paleidę programą 2000 m. sausio 1 d. 0 val., 0 min. 1 sek. turite gauti rezultatą:
365 23 59 58

180. SLAPTARAŠTIS.
Testo nr.
Pradiniai duomenys
Rezultatai
Paaiškinimai
1
 abc
slkslkslkslk		 ssssllllkkkk Rakto raidės išrikiuotos abėcėlės tvarka; Dalijant į grupes nelieka nė vienos nepilnos grupės
2
 klmno
cvbnmcvbnmcvbn		 cccvvvbbbnnnmm Rakto raidės išrikiuotos abėcėlės tvarka;
Keli atvejai, kai dalijant į grupes gaunamos nepilnos grupės
3
 klmno
cvbnmcvbnmcvb		 cccvvvbbbnnmm
4
 klmno
cvbnmcvbnmcv		 cccvvvbbnnmm
5
 klmno
cvbnmcvbnmc		 cccvvbbnnmm
6
 okmln
cvbnmcvbnmcvbnm		 vvvnnnbbbmmmccc Rakto raidės neišrikiuotos abėcėlės tvarka; Dalijant į grupes nelieka nė vienos nepilnos grupės
7
 septyni
Tikėjosi,*jog*pačios*
aplinkybės*viską*išaiškins.		 i,apėąks**ysiogskia.k*čls
*iTipabkšėjii*injoonvšs		 Koduojamas realus tekstas, kuriame yra lietuviškų raidžių, skyrybos ženklų, tarpų. Rakto bei teksto ilgiai artimi maksimaliems.
  Pastaba. 7 testo rezultatuose tarpai pažymėti * simboliu.

181. VARLIŲ KONCERTAS.
Testo nr.
Pradiniai duomenys
Rezultatai
Paaiškinimai
1
 2
8 8		 Koncertas įvyks po 0 val. ir 8 min.  Paprasčiausias atvejis: abu periodai sutampa
2
 3
2 3 5		 Koncertas įvyks po 0 val. ir 30 min.  Periodai neturi bendrų daliklių: kartotinis lygus periodų sandaugai
3
 6
12 15 20 10 6 30		 Koncertas įvyks po 1 val. ir 0 min.  Periodai turi bendrų daliklių
4
 5
18 7 3 2 4		 Koncertas įvyks po 4 val. ir 12 min.  Tikrinama, ar laikas teisingai perskaičiuojamas į valandas ir minutes
5
 10
11 12 13 14 15 16 17 18 19 20		 Koncertas įvyks po 3879876 val ir 0 min.  Šiuo testu tikrinamas sprendimo efektyvumas

Antrojo etapo uždavinių testai

Vyresniųjų grupė

182.  SEIFO KODAS.
Testo nr.
Pradiniai duomenys
Rezultatai
Paaiškinimai
1
2 0 0 2
 1 35 Lengvas atvejis
2
4 3 4 2
 23 1278  Tikrinama, ar randamas teisingas sprendinių skaičius
3
4 3 4 3
 24 1103
4
4 3 4 4
 23 1313
5
5 0 4 1
 234 10000 Tinka pirmasis penkiaženklis skaičius
6
6 3 4 8
 2337 100328 Tikrinamas sprendimo efektyvumas
7
7 2 6 10
 23377 1000152
8
8 1 1 1
 233766 10000376
9
9 3 2 4
 2337662 100000168

183. SANDAUGOS ĮSTRIŽAINĖSE
Pradinių duomenų lentelė (pirmas duomuo reiškia lentelės dydį, toliau pateikti lentelę sudarantys skaičiai)
1
2
3
4
5
6
4
7 8  9  1
4 5 35  9
1 3  3  4
1 9 10  1		 4
4  5 8  9
1 25 3  6
4 21 3 15
1  7 8  8		 6
1 5  8 9  5  1
4 4  6 7  8  9
1 5  6 8  4  5
1 2  8 9  6 10
4 5 15 9 10  5
4 5  7 6  5  8		 5
 4 5 2 9  7
 4 5 6 7  9
14 2 7 9 10
 1 5 8 9  6
 1 5 7 8  5		 2
14 10
21 15		 8
1 5 7 9  2 4 5 7
1 5 7 8  9 6 2 4
4 5 8 7 18 2 4 8
1 4 8 5  7 8 9 4
1 4 6 6  3 2 5 4
5 8 9 2 20 6 9 4
6 8 4 7  8 1 2 5
4 5 7 8  6 5 4 2

Rezultatų bei paaiškinimų lentelė
Testo nr.
Rezultatai/Galimi rezultatai
Paaiškinimai
1
 SANDAUGOS LYGIOS Pradinis kvadratas tenkina sąlygą; pradinio kvadrato kraštinė – lyginis skaičius
2
 4 Ieškomas kvadratas yra vienetinis;
3
  6 8  4
 8 9  6
15 9 10		 Ieškomo kvadrato (sprendinio) kairysis viršutinis kampas nesutampa su pradinio kvadrato kairiuoju viršutiniu kampu; egzistuoja vienintelis sprendinys;
4
  4 5 2
 4 5 6
14 2 7		 Ieškomo kvadrato kairysis viršutinis kampas sutampa su pradinio kvadrato kairiuoju viršutiniu kampu; egzistuoja vienintelis sprendinys; pradinio kvadrato kraštinė – nelyginis skaičius
5
 SANDAUGOS LYGIOS Kvadratas minimalaus dydžio
6
 16 2 4 8
 7 8 9 4
 3 2 5 4
20 6 9 4		 Kvadratas maksimalaus dydžio

184. KVADRATINĖ KOCH SALA.
Pradiniai duomenys bei rezultatai
1 testas; n = 2
2 testas; n = 3
3 testas; n = 5
4 testas; n = 7


Trečiojo etapo uždavinių testai

Pirmoji dalis

Jaunesniųjų grupė

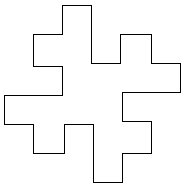
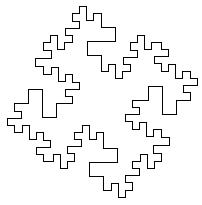
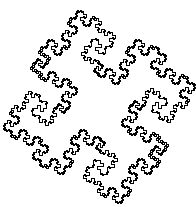
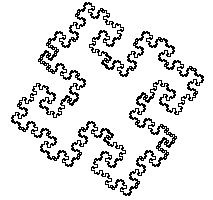
185. NAMŲ DAŽYMAS. Testams parinktos visos galimos n reikšmės.
Testo nr.
Pradinis duomuo
Rezultatas
1
1
2
2
2
3
3
3
5
4
4
8
5
5
13
6
6
21
7
7
34
8
8
55
9
9
89
10
10
144
11
11
233
12
12
377
13
13
610
14
14
987
15
15
1597
16
16
2584
17
17
4181
18
18
6765
19
19
10946
20
20
17711
21
21
28657

186. KARUSELĖS.
Testo nr.
Pradiniai 
duomenys
Rezultatai
Paaiškinimai
0
 24 22 12
23		 Sutampa su sąlygoje pateiktu pavyzdžiu
1
 20 32456 5
21		 Skaičius b nepakliūva į intervalą   [20, a);
2
 5382 9603 598
25		 Keletas didėjančių testų, kai pradiniai duomenys neviršija maxint
3
 17462 58 8731
21
4
 25116 32174 12558
25
 5
 188202
188202		 1
23		 Sutampa vagonėlių skaičius abiejose karuselėse
6
 1766232 35853 936 
23		 Didesnis testas 
7
 12345687 254867 12345687 
20		 a ir b yra tarpusavyje pirminiai 
1 dalis) aplankomi visi vagonėliai; 
2 dalis) tinka mažiausia galima b reikšmė
8
 2147395600 2147349260 46340
23		 Didėjantys testai; Skaičiai a ir b artimi maxlongint; bandantskaičiuoti mbk(a, b) įvyktų perpildymas;
9
 2146892910 20 214689291
37


 
 

Trečiojo etapo uždavinių testai

Pirmoji dalis

Vyresniųjų grupė

187. BRANGAKMENIAI.
Testo nr.
Rezultatas
Paaiškinimai
1
1000
 Viršūnė ir aklavietė
2
472
 Nedidelis labirintas iš 24 elementų
3
7
 Nedidelis labirintas iš 25 elementų
4
18
 Didesnis labirintas iš 100 elementų
5
96
 Labirintas iš 1000 elementų
6
5
 „Platus“ labirintas. Iš įėjimo eina 3 šakos, o nuo jų atsišakoja
7000 aklaviečių
7
8595
 Labirintas iš 8000 elementų
8
14421
 Labirintas iš 10000 elementų
9
9001
 Iš viršūnės išeina 5 šakos ir po to jos nesišakodamos tęsiasi
gilyn. 9001 elementas
10
12
 Viena ilga šaka iš 10000 elementų

188. KANDIDATAS Į PREZIDENTUS
Testo nr.
Pradinis dienų skaičius
Ilgiausio nemažėjančio sąrašo ilgis
Paaiškinimai
1
6
4
 Sutampa su sąlygoje pateiktu pavyzdžiu
2
10
10
 Rezultatas sutampa su pradiniu sąrašu
3
10
1
 Pradiniame sąraše reitingai tik mažėja
4
30
11
 Likusieji testai tikrina sprendimo efektyvymą;


 
 

Trečiojo etapo uždavinių testai

Antroji dalis

Jaunesniųjų grupė

189.  MAGIŠKI KVADRATAI.
Testo nr.
Pradiniai duomenys
/kvadrato dydis
Rezultatai
Paaiškinimai
1
 2
23  23
23  25		 GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ
2 2 23		 Atskiras atvejis n = 2; Trys iš keturių skaičiai vienodi
2
 2
23  25
23  25		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Atskiras atvejis n = 2; Atstatyti negalima
3
 3
8 1 6
3 5 7
4 9 2		 MAGIŠKASIS KVADRATAS Kvadratas magiškas
4
 3
8 2 6
3 5 7
4 9 2		 GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ
1 2 1		 Galima atstatyti. Nesutampa 1 eilutės ir 1 stulpelio sumos
5
 3
14  7 11
 8 11 14
10 15  8		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 1 eilutės ir 1 stulpelio, 1 įstrižainės sumos; Yra keli sankirtos taškai; Yra tik 2 skirtingos sumos
6
 3
8 1 6
3 5 7
4 9 3		 GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ
3 3 2		 Galima atstatyti. Nesutampa 1 eilutės ir 1 stulpelio, 1 įstrižainės sumos
7
 3
13  7 11
 8 11 14
10 15  8		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 1 eilutės ir 1 stulpelio, 2 įstrižainės sumos; Yra daugiau nei 2 skirtingos sumos
8
 3
8 1 6
3 2 7
4 9 2		 GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ
2 2 5		 Galima atstatyti. Nesutampa 1 eilutės ir 1 stulpelio, 2 įstrižainių sumos
9
 4
16 2 3 13
5 11 10 3
9 7 6 12
4 9 15 6		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 1 eilutės ir 1 stulpelio, 1 įstrižainės sumos; Kertasi viename langelyje, Yra daugiau nei 2 skirtingos sumos
10
 4
16 2 12 4
1 11 10 17
9 7 6 12
13 14 6 1		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 1 eilutės ir 1 stulpelio sumos; Būtų galima, jei kvadratą galėtų sudaryti neigiamas skaičius
11
 4
3 9 7 10
8 8 5 8
9 5 12 5
9 7 7 6		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 1 eilutės ir 1 stulpelio sumos. Atstatant būtų išgadinta įstrižainė.
12
 4
3 9 7 15
8 8 10 8
8 15 10 1
15 2 7 10		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa tik dviejų įstrižainių sumos
13
 4
3 9 7 10
8 8 5 8
9 5 10 5
9 7 7 6		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa vienos įstrižainės suma
14
 4
10 7 9 3
8 5 8 8
5 10 5 9
6 7 7 9		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa vienos įstrižainės suma
15
 4
3 9 7 10
8 8 5 8
9 5 11 5
9 7 7 6		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 1 stulpelis, 1 eilutė, 1 įstrižainė. Tos įstrižainės suma skiriasi nuo eilutės ir stulpelio sumos
16
 4
10 7 9 2
8 5 8 8
3 12 5 9
8 5 7 9		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti.Tas pats kas 15 testas tik paimta kita įstrižainė
17
 4
6 16 3 4
9 7 10 3
4 5 7 13
10 5 5 9		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 2 stulpeliai
18
 4
 6 16  3 4
 9  7 10 8
 4  5  7 8
10  1  9 9		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 2 eilutės
19
 4
 6 16  3  4
 9  7 10  8
 4  5  7 18
10  1  9  9		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 2 eilutės, 1 stulpelis
20
 4
 6 16  3  4
 9  7 10  3
 4  5  7 13
10  3 10  9		 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 1 eilutė, 2 stulpeliai
21
 5
17 24  1  8 15
23  5  7 14 16
 4  6 13 20 22
10 12 19 21  3
11 18 25  2  9		 TAI MAGIŠKASIS KVADRATAS Magiškas kvadratas
22
 10 NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU Negalima atstatyti. Nesutampa 3 stulpeliai
23
 11 GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ
6 6 61		 Galima atstatyti. Nesutampa 1 stulpelio, 1 eilutės, 2 įstrižainių sumos
24
 13 GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ
3 5 12		 Galima atstatyti. Nesutampa 1 stulpelio, 1 eilutės sumos
25
 20 GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ
2 19 362		 Galima atstatyti. Nesutampa 1 stulpelio, 1 eilutės, 1 įstrižainės sumos
26
 30 GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ
15 3 815		 Galima atstatyti. Nesutampa 1 stulpelio, 1 eilutės sumos
27
 40 GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ
39 2 79		 Galima atstatyti. Nesutampa 1 stulpelio, 1 eilutės, 1 įstrižainės sumos
28
 50 GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ
38 13 313		 Galima atstatyti. Nesutampa 1 stulpelio, 1 eilutės sumos
Pastaba. 23–28 testai tikrina sprendimo efektyvumą

190. SĄMOKSLAS
Testo nr.
Pradiniai duomenys
Rezultatai
Paaiškinimai
0
 GINKLAI YRA!
7
GUDASAS
E MIE !
NYIAGON
AAARBDK
RNAAAKI
ŠLVA!MV
!USSO !		 OXXXXXX
XXXOXXX
XXXXXXO
XXXXXXX
XXXXXOX
XOXOXXX
XXXXXXX		 Pavyzdys, pateiktas prie uždavinio sąlygos.
1
 LABAS, AS KRABAS.*
5
LI@ A
BASK,
UR( (
AABAS
.S(E*		 OXXXO
OOOXO
XXXOX
XOXXX
XOXXX		 Paprastas testas, su 5x5 raidžių lentele.
2
 MYLIU TETI, MYLIU MAMA, O LABIAUSIAI MIF DEKANA!
Pastaba: aukščiau esantis tekstas pateikiamas vienoje eilutėje 
8
M2O YLLM
IFAU B I
9T8AEUTI
^SI8A,I 
 MMY0LI=
IFU  ,DW
MEA$KMYA
,NAA, S!		 OXXXOXOX
OXXOXXOX
XOXXOXOO
XXXXXOXO
XOXOXOOX
XXOXOXXX
OXOXXOXX
XXOXOOXX		 Šiek tiek didesnis testas
3
 Tekstas: 100 A raidžių, raidžių lentelė: 10x10   Apsukus tinklelį, skylutės dažnai sutampa, t.y.,ta pati raidė perskaitoma 2 kartus.
4
 Tekstas: JAU!, raidžių lentelė: 15x15  
Imami didesni testai, kad ištirti sprendimų efektyvumą.
5
 Ilgas prasmingas tekstas (100 simb.), raidžių lentelė:25x25  
6
 Ilgas tekstas iš daug vienodų raidžių, raidžių lentelė:38x38  
7
 72 simb. tekstas, raidžių lentelės dydis: 50x50  
8
 100 simb tekstas iš vienodų simbolių, raidžių lentelė 50x50 sudaryti iš keletos skirtingų raidžių.  
9
 100 simb. prasmingas tekstas, raidžių lentelė 50x50, laisvos vietos užpildytos tarpais.   

191. B. BITAS KURIA TEKSTŲ REDAKTORIŲ.
Testo nr.
Rezultatas
Paaiškinimai apie pradinius duomenis
1
1
 Trumpas testas, kai tekstą sudaro viena eilutė ir fragmentas jame sutinkamas vieną kartą
2
0
 Duoto fragmento tekste nėra
3
3
 Fragmente nėra didžiųjų raidžių
4
4
 Fragmente yra didžiųjų raidžių
5
14
 Yra atvejų kai fragmentas persikloja
6
4
 Fragmentas sutinkamas ir žodžiuose, kurie yra keliami į kitą eilutę
7
12
 Maksimalus teksto eilučių skaičius 

192. ŽIEMA FANTAZIJOS KARALYSTĖJE
Nr.
Kelio ilgis
Paaiškinimai
1
10
 2 miestai ir kelias tarp jų
2
59
 12 miestų. Reikia panaudoti visus kelius.
3
22
 8 miestai.
4
56
 12 miestų.
5
4900
 50 miestų, visi keliai vienodo ilgio.
6
3507
 75 miestai, 2000 kelių.
7
13377
 100 miestų, 500 kelių.
8 
11319
 120 miestų, 6000 kelių.
9
11
 3 miestai, 3 keliai.
10
23
 5 miestai, 7 keliai.

193. MAŠININIŲ KODŲ INTERPRETATORIUS
Pastaba. Taupant vietą atminties laukelių reikšmės byloje PROG.EXC surašytos į vieną eilutę.
Testo nr.
INT.DAT
PROG.EXC
Paaiškinimai
1
 8000 16 0 603
0 701 1000000000 0 702 2000000000 ... 0
800 100000000000 3 1000 701 3 1000 702 ... 3 1000 799 3 1000 800 7 1000 14 		 Į atminties langelius nuo L[701] iki L[800] surašomi skaičiai nuo 1000000000 iki 100000000000; Randama bei išspausdinama jų suma; Ji saugoma laukelyje L[1000] ir lygi 5050000000000
2
 3000 15 0 603
0 2001 1 0 2002 2 0 2003 3 ... 0 2100 100 5 1000 2001 3 1000 2002 5 1000 2003 3 1000 2004 ... 5 1000 2099 3 1000 2100 7 1000 14		 Į atminties langelius nuo L[2001] iki L[2100] surašomi skaičiai nuo 1 iki 100; Randama bei išspausdinama reiškinio -1+2-3+4...-97+98-99+100 suma; Ji saugoma laukelyje L[1000] ir lygi 50
3
 6000 15 0 54
6 5693 6 5694 6 5695 6 5696 6 5697 6 5698 6 5699 6 5700 6 5701 6 5702 3 100 5693 3 100 5694 3 100 5695 3 100 5696 3 100 5697 3 100 5698 3 100 5699 3 100 5700 3 100 5701 3 100 5702 7 100 14 		 Programa įveda dešimties ir randa bei išspausdina jų sumą; Įvesti skaičiai patalpinami laukeliuose nuo L[5693] iki L[5702], suma patalpinama laukelyje L[100]
4
 40 15 0 11
6 30 3 31 30 12 0 30 7 31 14		 Programa ciklu įveda nenulinių skaičių seką, kurios pabaiga – nulis. Suskaičiuojama bei išspausdinama sekos narių suma .
L[30] – šiame atminties langelyje saugomas naujai perskaitytas sekos narys
L[31] – šiame atminties langelyje saugoma sekos narių suma; 
5
 60 15 0 22
6 51 11 19 51 0 50 1 9 50 51 12 0 50 2 52 1 13 0 7 52 14		 Programa ciklu  įveda nenulinių skaičių seką, kurios pabaiga – nulis. Suskaičiuojama bei išspausdinama kiek sekoje buvo didesnių už 1 skaičių.
L[50] – šiame atminties langelyje saugomas vienetas;
L[51] – šiame atminties langelyje saugomas naujai perskaitytas sekos narys;
L[52] – šiame atminties langelyje saugomas didesnių už 1 sekos narių skaičius;


 

194. KELIAUTOJAS.
Testo nr.
Miestai
Maršrutai
Maršrutų
ilgiai
Maršrutų 
tinkamumas
Trumpiausias  ir
ilgiausias maršrutai
0
 2
123 456
789 654		 1 2 0
2 1 0		 1389.62 km.
1389.62 km.		 Tinkamas
Tinkamas		 2 1– 1389.62km
2 1– 1389.62km
1
 5
1 2
3 1
4 2
5 4
3 6		 1 2 3 4 5 0
1 5 2 4 3 0
5 2 3 5 1 0
5 3 2 4 1 0
4 3 5 1 2 0
5 2 4 1 0		 13.19 km.
18.31 km.
19.48 km.
18.09 km.
16.67 km.
17.55 km.		 Tinkamas
Tinkamas
Netinkamas
Tinkamas
Tinkamas
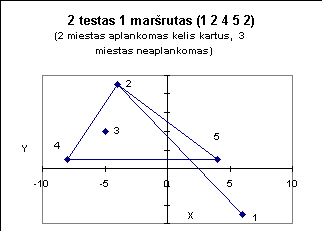
Netinkamas		 1 2 3 4 5–13.19 km
1 5 2 4 3–18.31 km
2
   5
 6 -5
-4  9
-5  4
-8  1
 4  1		 1 2 4 5 2 0
2 3 4 1 4 0
3 5 3 2 0
4 2 5 3 2 0
5 2 4 5 2 0		 66.67 km.
48.75 km.
29.17 km.
43.79 km.
54.89 km.		 Netinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas		 Neįvestas nė vienas 
tinkamas maršrutas
3
 4
1 1
2 2
3 3
3 1		 1 4 3 2 0
3 1 2 4 0
1 4 2 3 0
2 4 3 1 0
2 1 3 0		 6.83 km.
7.66 km.
7.66 km.
7.66 km.
5.66 km.		 Tinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas		 1 4 3 2 - 6.83 km
1 4 3 2 - 6.83 km
4
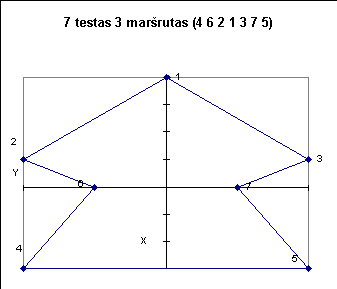
 7
-1  10000
 1  10000
-1   9999
 0      0
 1  -9999
 1 -10000
-1 -10000		 1 2 4 5 6 3 7 0
6 3 1 5 2 4 7 0
6 1 2 7 5 3 4 0
2 4 5 6 7 1 3 0
7 4 6 5 1 3 2 0
3 1 2 4 5 6 7 0
2 1 3 4 5 7 6 0		 80000.00 km.
80000.00 km.
80001.24 km.
40005.24 km.
60003.24 km.
40004.00 km.
40005.24 km.		 Netinkamas
Tinkamas
Netinkamas
Netinkamas
Netinkamas
Tinkamas
Netinkamas		 3 1 2 4 5 6 7 - 40004.00 km
6 3 1 5 2 4 7 - 80000.00 km
5
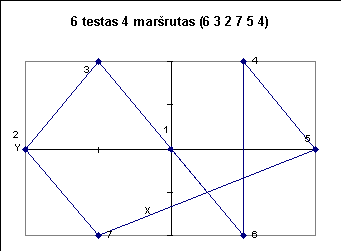
 10
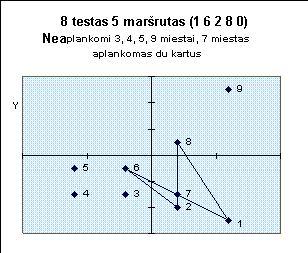
-7637 -8618
 4054  5405
-2381  8562
-9539  9963
-7078 -2835
 1461  2689
-5846 -3862
 4525  -417
 9542  2811
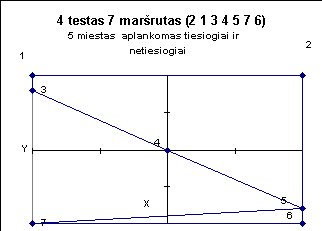
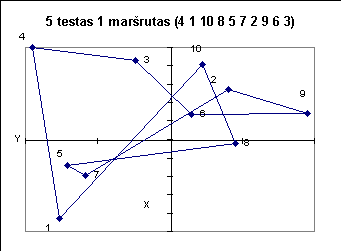
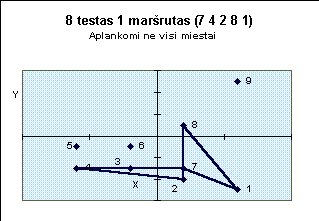
 2222  8164		 4 1 10 8 5 7 2 9 6 3 0
3 5 6 4 10 8 1 2 7 9 0
8 3 7 6 1 10 9 2 4 5 0
6 5 4 10 3 7 1 8 9 2 0
1 5 2 9 4 3 8 7 6 10 0
7 3 4 6 8 2 9 1 5 10 0
7 3 2 5 6 4 8 9 1 10 0
4 10 3 8 1 2 6 5 9 7 0
1 10 7 6 2 8 9 3 4 5 0
6 5 9 3 2 1 4 8 10 7 0		 102507.12 km.
132963.41 km.
122376.16 km.
88160.30 km.
110461.97 km.
104982.43 km.
135297.51 km.
123331.66 km.
98694.55 km.
135722.97 km.		 Tinkamas
Tinkamas
Tinkamas
Tinkamas
Tinkamas
Tinkamas
Tinkamas
Tinkamas
Tinkamas
Tinkamas		 6 5 4 10 3 7 1 8 9 2 - 88160.30km;
6 5 9 3 2 1 4 8 10 7 - 135722.97 km;
6
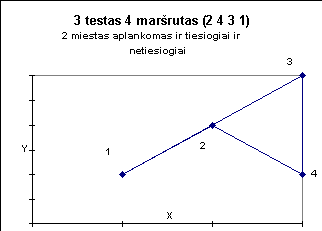
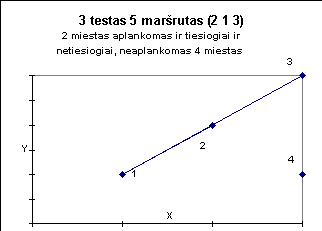
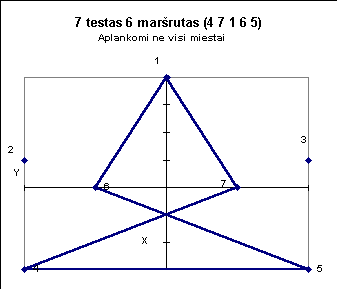
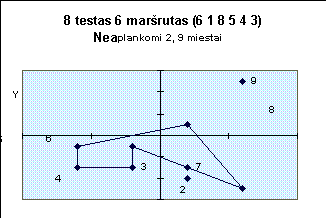
    7
   0    0
-100    0
 -50  100
  50  100
 100    0
  50 -100
 -50 -100		 1 2 3 7 5 6 4 0
2 5 4 3 7 6 0
3 6 5 4 7 2 0
6 3 2 7 5 4 0
1 7 6 5 0		 1015.69 km.
892.08 km.
894.43 km.
939.29 km.
423.61 km.		 Tinkamas
Tinkamas
Netinkamas
Tinkamas
Netinkamas		 2 5 4 3 7 6 0 - 892.08 km;
1 2 3 7 5 6 4 - 1015.69 km;
7
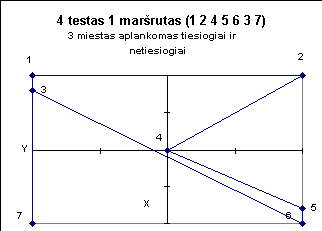
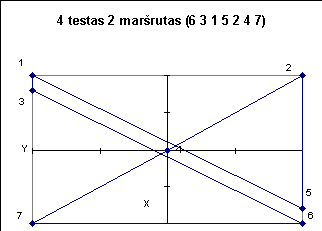
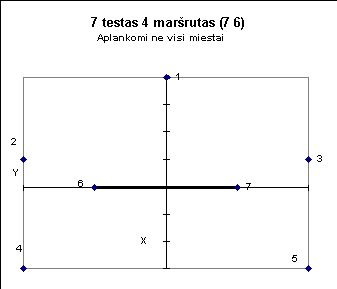
  7
 0  4
-2  1
 2  1
-2 -3
 2 -3
-1  0
 1  0		 6 7 6 7 0
3 4 5 0
4 6 2 1 3 7 5 0
7 6 0
2 3 5 4 2 1 0
4 7 1 6 5 0		 8.00 km.
13.66 km.
20.36 km.
4.00 km.
23.21 km.
20.73 km.		 Netinkamas
Netinkamas
Tinkamas
Netinkamas
Netinkamas
Netinkamas		 4 6 2 1 3 7 5 - 20.36 km;
4 6 2 1 3 7 5 - 20.36 km;
8
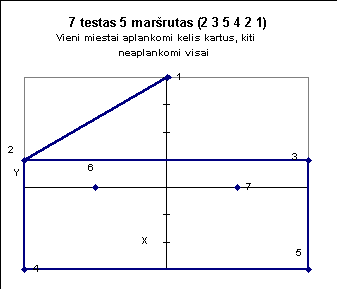
 9
 6 -5
 2 -4
-2 -3
-6 -3
-6 -1
-2 -1
 2 -3
 2  1
 6  5		 7 4 2 8 1 0
2 5 4 8 1 6 0
1 7 2 5 4 6 0
8 1 5 4 6 7 0
1 6 2 8 0
6 1 8 5 4 3 0
9 6 1 5 4 0
2 5 4 6 1 8 9 0		 32.75 km.
40.64 km.
29.43 km.
34.80 km.
26.16 km.
32.40 km.
48.02 km.
46.68 km.		 Netinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas		 Neįvestas nė vienas 
tinkamas maršrutas
9
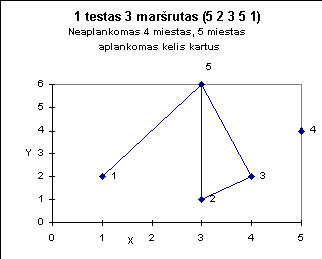
    15
-1382  7601
 2764  7601
 6219  5528
 1382  4837
-4837  3455
 -691  2073
 2073  2073
 6910  1382
-8983     0
-4837 -1382
-2073 -1382
 7601 -1382
 1382 -3455
 4146 -3455
 1382 -6219		 15 7 6 4 2 8 12 14 5 9 10 1 11 13 3 0
14 3 4 9 1 11 5 8 2 13 15 7 6 12 10 0
6 12 5 14 7 4 11 10 8 1 2 13 3 15 0
3 9 4 8 7 10 11 1 2 13 6 5 14 0
9 14 12 13 15 7 5 10 6 11 3 4 8 0
9 7 4 6 11 13 15 14 12 8 1 3 5 0
11 5 6 13 12 9 10 0
6 7 0
1 7 13 9 5 0		 98652.56 km.
125906.97 km.
121467.33 km.
104632.67 km.
94398.93 km.
73743.37 km.
46176.35 km.
5528.00 km.
33809.34 km.		 Tinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas
Netinkamas		 15 7 6 4 2 8 12 14 5 9 10 1 11 13 3 - 98652.56 km;
15 7 6 4 2 8 12 14 5 9 10 1 11 13 3 - 98652.56 km;

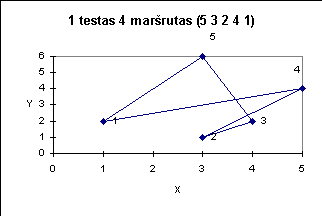
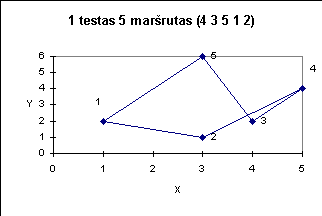
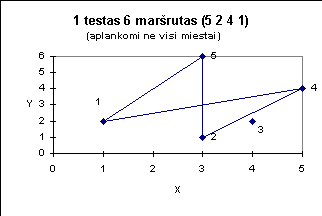
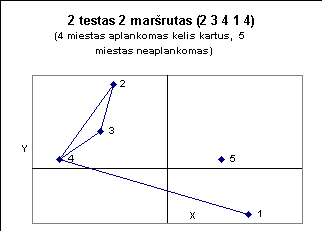
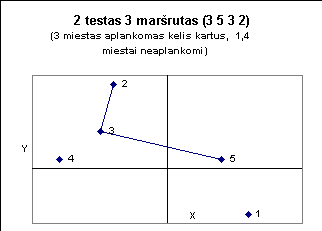
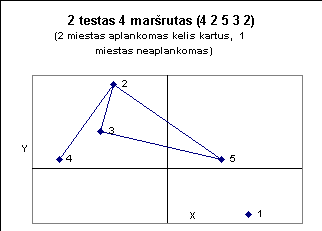
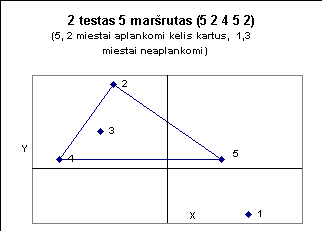
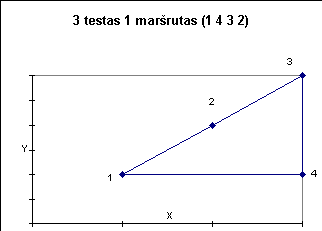
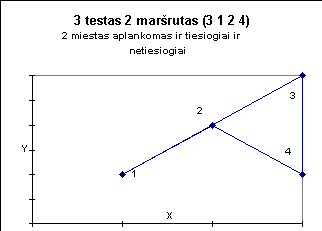
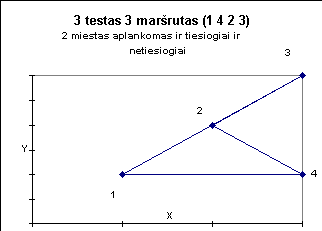
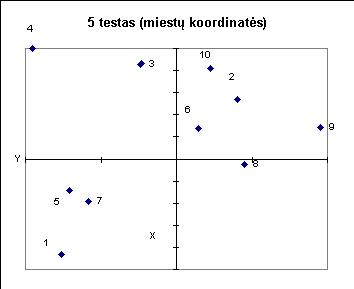
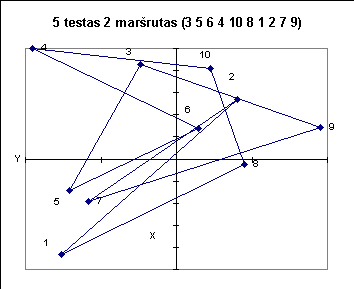
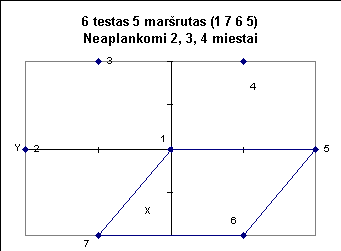
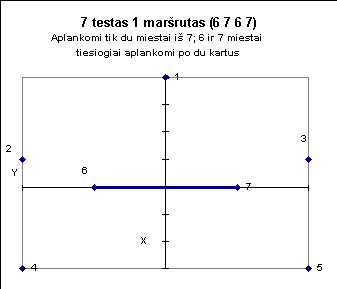
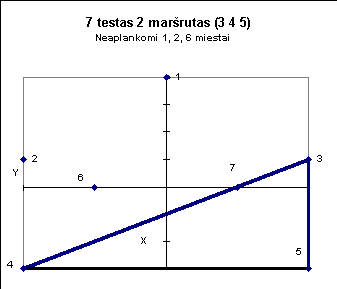
Žemiau pateiktuose paveiksluose iliustruojami kai kurie testai.
 


 
 

Trečiojo etapo uždavinių testai

Antroji dalis

Vyresniųjų grupė

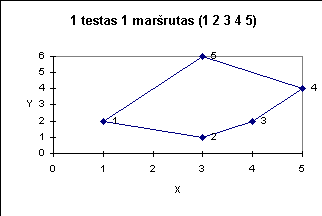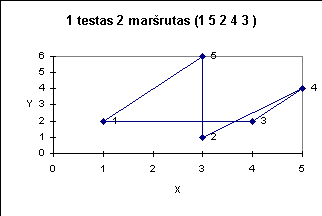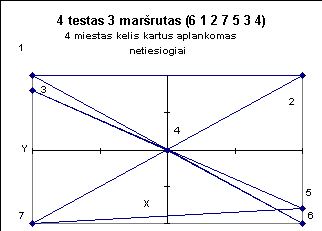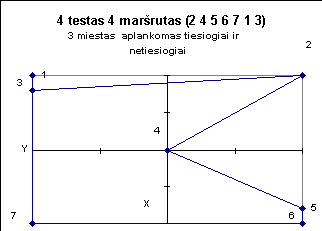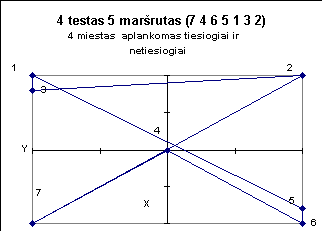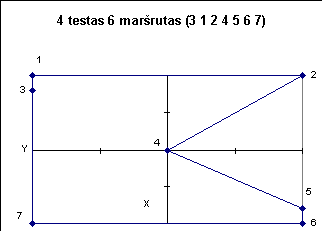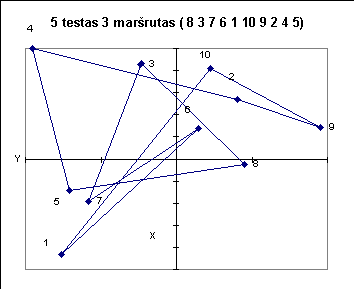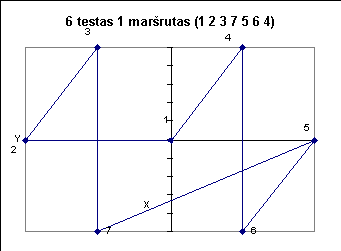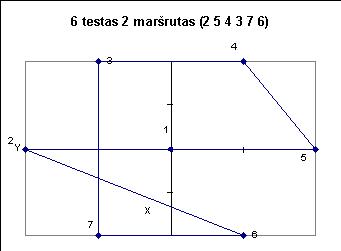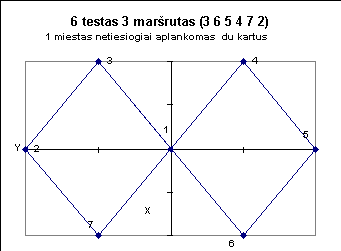195. PASKALIO PROGRAMŲ PAKAVIMAS
Testo nr.
Pakuojamos
programos dydis
Supakuotos programos dydis
Kurią dalį 
pradinės bylos (procentais)
užima
suspausta byla
Paaiškinimai
0
 78
61
78%
 Tuščia programa, vienas komentaras
1
 2195
1029
47%
 Labai mažai tarpų, tačiau daug bazinių Turbo Paskalio žodžių, kintamųjų vardai labai panašūs į tipus; byla baigiama simboliu, kurios kodas yra 26.
2
 8437
2410
28%
 Šiek tiek tarpų tarp kiekvieno žodžio
3
 12318
6843
55%
 Visai nėra tarpų, kiekvienas žodis yra naujoje eilutėje
4
 28251
11350
40%
 Tvarkingas modulis, iš eilės kartojasi ne tik tarpai, bet ir pabraukimo simboliai; byla baigiama simboliu, kurios kodas yra 26.
5
 48608
19510
40%
 Nedaug Paskalio bazinių žodžių, ilgi kintamųjų vardai, daug komentarų ir skaičių
6
 64774
18561
29%
 Maksimalus testas, prieš kiekvieną sakinį pridėta daug tarpų
7
 64906
30825
47%
 Maksimalaus dydžio testai, sukurti iš mokinių sprendimų
8
 64828
30666
47%
9
 64868
30190
46%


 

196.  LYGIAGRETŪS SKAIČIAVIMAI
Testo nr.
N ir K reikšmės
Gautų blokų skaičius
Paaiškinimai
1
 1000 100
1
 Visos    komandos  priklausomos.Gaunamas  vienas   blokas.
2
 1000 997
997
 Visos komandos atliekamos su skirtingais atminties laukeliais
3
 1000 1000
2
 Pirmosios 500 komandų pakliūna į vieną bloką, likusios – į antrą.
4
 1000 10000
10
 10  blokų   po  1000    komandų
5
 1000 10000
10
 Testas,  sugeneruotas ats.  sk.   gener. pagalba.

197. GALVOSŪKIS

Testo nr.
Pradinių duomenų aprašymas
Rezultatas
Paaiškinimai
1
 3 3 
5 12 1 
7 79 13 
4 11 2
2
 Testas su mažiausiomis m ir n reikšmėmis;
2
 5 5 
2 1 5 1 2 
2 2 8 2 2 
1 7 13 20 2 
1 4 8 19 2 
2 11 10 1 2
6
 Keli didėjantys testai, tikrinantys sprendimo efektyvumą
3
 n = 6, m = 10
12
4
 n = 15, m = 14
40
5
 n = 25, m = 30
121
6
 n = 81, m = 72. 
1944
 Visa lentelėsudaryta  iš „nepersidengiančių“ lygybių
7
 n = 60, m = 64. 
0
 Nėra nė vienos lygybės.
8
 6 5 
1 2 3 1 2 
1 2 3 1 2 
1 2 3 1 2 
1 2 3 1 2 
1 2 3 1 2 
1 2 3 1 2
10
 Kiekvienas pradinės lentelės skaičius įeina į kažkurią lygybę
9
 n = 50, m = 50
391
 Labai dideli testai tikrinantys sprendimo efektyvumą
10
 n = 100, m = 100
1389

198. APLINK ŽEMĘ PER 80 DIENŲ
Testo nr.
Paaiškinimai
1
 Panašus testas į pvz., tik iš pradinio miesto iškeliaujama 0:0, atvykstama po 2 parų ir 46 minučių.
2
 50 miestų ir 30 maršrutų. Iš pradinio miesto reikia iškeliauti 0:0. Reigalingi 6 persėdimai.
3
 50 miestų ir 30 maršrutų. Testas sukurtas su ats. generatoriumi. Reikalingi 3 persėdimai.
4
 Nedidelis testas: 11 miestų, 3 maršrutai. Apkeliauti negalima, nes negalima grižti į tą patį miestą, tačiau egzistuoja ciklai, kuriais galima keliauti ratu.
5
 6 miestai, 3 maršrutai. Pradedama keliauti iš pirmo miesto. Apkeliauti negalima.
6
 Testas toks pat, kaip ir 5 testas, tik keliauti pradedama iš antro miesto. Apkeliauti galima su 1 persėdimu.
7-10
 Atsitiktiniai maksimalus testai, skirti patikrinti sprendimo efektyvumą.

199.  B. BITAS KURIA TEKSTŲ REDAKTORIŲ.
Testo nr.
 n bei m 
reikšmės
Rezultatai
Paaiškinimai apie pradinius duomenis
1
 1 13 1 25
2 1
8 51
8 69
10 1		 Trumpas prasmingas tekstas, fragmentą sudaro tik viena eilutė
2
 13 38 1 1 Trumpas prasmingas tekstas. Fragmentą sudaro keliolika  eilučių. Jis sutinkamas tik vieną kartą nuo pirmojo teksto simbolio
3
 13 38 1 2 Analogiškas tekstas tik fragmentas sutinkamas ne nuo pirmojo simbolio
4
 11 50 1 2
38 28		 Analogiškas tekstas tik fragmentas sutinkamas du kartus ir ne nuo pirmojo simbolio
5
 50 350 50 79
100 78		 Fragmentas F yra atsitiktinė simbolių seka S + atsitiktinis simbolis T: TS 
Tekstas yra pavidalo:   TT...TS
6
 50 500 450 72 Fragmentas F yra atsitiktinė simbolių seka S + atsitiktinis simbolis T + ta pati atsitiktinė seka T: TST 
Tekstas yra pavidalo:   TT...TST...TTTT
7
 250 2500 1001 1
2251 1		 Fragmentas yra pavidalo: aaaaaa.....aaaab; 
Tekstas yra pavidalo: aaa....aaaabaaaa....aaaab;
8
 250 2500 1001 3
2251 2		 Fragmentas yra pavidalo abab....abb; 
Tekstas yra pavidalo abab...abababbabab...abababb
9
 250 8000 347 2
2318 2
6838 2		 Sprendimo efektyvumą tikrinantys testai. Testas bei fragmentas yra pavidalo: 

abababababababa..... 

kur kai kuriose vietose raidė „a“ pakeista į raidę „b“ (t. y. paeiliui gaunamos trys b raidės: „bbb“
10
 250 25000 347 2
2318 2
6838 2
8369 2
10340 2
14860 2
16391 2
18362 2
22882 2
24413 2
11
 1 2 0 Trumpas testas, kai ieškomasis fragmentas nerastas

200. ŠAŠKĖS
Testo nr.
Lentos dydis bei šaškių skaičius lentoje
Rezultatas
1
 Dydis: 4, šaškių skaičius: 5
1
2
 Dydis: 6, šaškių skaičius: 7
2
3
 Dydis: 9, šaškių skaičius: 11
2
4
 Dydis: 10, šaškių skaičius: 13
3
5
 Dydis: 15, šaškių skaičius: 65
7
6
 Dydis: 40, šaškių skaičius: 372
18
7
 Dydis: 50, šaškių skaičius: 626
24
8
 Dydis: 50, šaškių skaičius: 608
23
9
 Dydis: 50, šaškių skaičius: 614
23
10
 Dydis: 60, šaškių skaičius: 901
29

Pastaba. Testai parinkti didėjančiai. Jie tikrina sprendimo efektyvumą.

201. MAŠININIŲ KODŲ INTERPRETATORIUS.
Testo nr.
n, k, R, m reikšmės
Iš ekrano įvedami duomenys
Rezultatai
Paaiškinimai
1
 100 32 0 69 FFF0
10		 FFF3
7
10000
FFEC		 Atliekami tokie veiksmai:
 begin
    readln(a);
    readln(b);
    a:=a+3;
    b:=b-9;
    c:=a+b;
    d:=a-b;
    writeln(a);
    writeln(b);
    writeln(c);
    writeln(d);
  end.
2
 1FFFF
10001		 20002
FFF8
2FFFA
1000A
3
 100000 48 0 21 1FFABCDEF
1FFABCDEF		 3FF579BDE
0
4
 FFFFFFFFFFF
FFFFFFFFFF0
1FFFFFFFFFFEF
F
5
 FFFFF
FF00		 10FEFF
F00FF
6
 8192 64 2 49 FFFFFFFFFFFF
FFFFFFFFFFF		 1
0
0
7
 FFFFFFFFFFF
FFFFFFFFFFFF		 0
0
1
8
 FFFFFFFFFFFF
FFFFFFFFFFFF		 0
1
0
9
 4096 128 16 53 FFFFFFFFFFFFF
FFFFFFFFFFFF		 Paskutinis sk 10
10
 10000 32 10 43 Įvedimo iš ekrano nėra 37