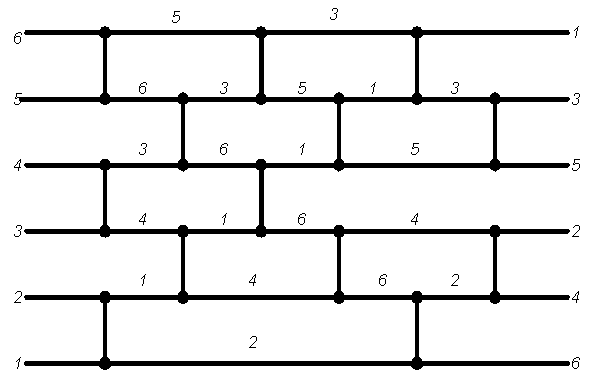
1 (234). LYGIAGRETUS RIKIAVIMAS. (teorinis
uždavinys). Žemiau pateiktas paveikslas parodo kaip gaunamas rezultatas.

2(235). ROMĖNIŠKI SKAITMENYS.
|
|
|
|
|
|
|
I | 1 | Mažiausias romėniškas skaičius |
|
|
MMMCMXCIX | 3999 | Didžiausias romėniškas skaičius |
|
|
MDCLXVI | 1666 | Nėra nei pasikartojančių skaitmenų, nei mažesnių skaitmenų prieš didesnius |
|
|
DCXXXVII | 637 | Yra pasikartojančių skaitmenų, tačiau nėra mažesnių skaitmenų prieš didesnius |
|
|
MCDIX | 1409 | Yra mažesnių skaitmenų prieš didesnius, tačiau nėra pasikartojančių skaitmenų |
|
|
MMMCCXLV | 3245 | Yra ir mažesnių skaitmenų prieš didesnius, ir pasikartojančių skaitmenų |
|
|
MMDLXIX | 2569 | Atsitiktinis testas |
|
|
MMCMLXXIX | 2979 | Atsitiktinis testas |
3 (236). TRIŽENKLIAI SKAIČIAI.
|
|
|
|
|
|
|
1 5 6 9 4 2 5 1 4 8 9 1 2 3 -1 |
|
Nė vienas triženklis skaičius nepasikartoja kelis kartus |
|
|
8 8 8 8 8 8 8 8 8 8 8 8 8 8 -1 |
|
Visi sekos nariai yra vienodi skaitmenys |
|
|
5 5 4 4 5 4 5 5 4 5 5 4 4 5 4 5 4 4 4 5 5 4 4 5 4 4 -1 |
|
Seka sudaryta iš dviejų skirtingų skaitmenų (bus nemažai pasikartojančių triženklių skaičių) |
|
|
4 0 2 5 8 0 0 5 4 8 0 0 0 4 5 8 7 4 1 5 4 0 1 4 0 1 -1 |
|
Sekoje yra nulių (t.y. sujungę tris gretimus sekos narius gausime ne triženklį skaičių) |
|
|
4 1 5 7 8 9 5 1 2 5 4 1 5 8 9 7 8 4 5 4 1 5 4 8 5 7 -1 |
|
Atsitiktinis testas |
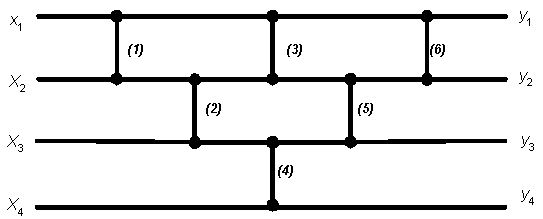
Šis rikiavimo tinklas atitinka rikiavimą sukeitimu. Įvykdžius 1, 2 ir 4 komparatorius didžiausias sekos narys nuskęs žemyn ir y4 reikšmė taps lygi didžiausiam sekos nariui. Įvykdžius 3 ir 5 komparatorius y3 reikšmė taps lygi antrajam didžiausiam sekos nariui. 6-asis komparatorius teisinga tvarka surikiuos pirmuosius du sekos narius.
Šio tinklo žingsnių skaičius lygus 5. Deja, tai nėra minimalus žingsnių skaičius.
Žemiau pateikiame keturių žingsnių tinklą, rikiuojantį seką iš keturių narių:
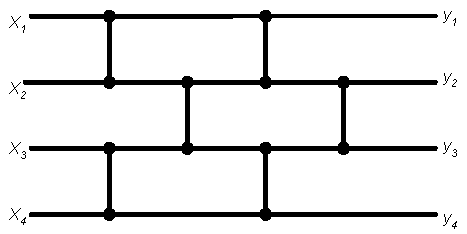
Iš pirmo žvilgsnio nėra akivaizdu, ar šis tinklas teisingai rikiuoja seką. Tuo galima įsitikinti tik atidžiau panagrinėjus tinklą.
Vertintojams gali tekti nemažai padirbėti norint įvertinti moksleivių sukurtus tinklus. Todėl pateikiame keletą pastabų bei pasiūlymų:
Atsakymas:optimalus keturių skaičių rikiavimo tinklas
turi keturis žingsnius; galimas sprendimas pateiktas aukščiau esančiame
paveiksle
2 (238). DANGORAIŽIS.
|
to nr. |
nis duo- muo |
|
Paaiškinimai |
|
|
12 | 1 5 2 1 1 1 1 1 1 1 | Paprastas atvejis |
|
|
635 | 123 234 234 230 224 224 159 123 123 123 | Du gretimi n |
|
|
636 | 123 234 234 231 224 224 161 123 123 123 | |
|
|
4500 | 1291 2400 2400 2400 1901 1301 1300 1300 1300 1300 | n baigiasi nuliais |
|
|
6002 | 1696 2801 2801 2800 2800 2800 1803 1800 1800 1800 | n viduryje yra keli nuliai |
|
|
7821 | 2262 3373 3364 3362 3362 3362 3362 3184 2284 2262 | Atsitiktinis testas |
|
|
10548 | 3653 4764 4215 4215 4214 4154 4105 4105 4105 4104 | n viduryje yra vienas nulis |
|
|
15648 | 5624 12384 6735 6735 6734 6374 5674 5625 5625 5624 | Atsitiktinis testas |
|
|
22222 | 8642 19753 11115 8642 8642 8642 8642 8642 8642 8642 | Visi n skaitmenys vienodi |
|
|
32089 | 12598 23619 22709 14709 12619 12619 12619 12619 12619 12609 | n arti viršutinės ribos |
3 (239). JANGO LENTELĖ.
Visiems testams pradiniai duomenys bus tokie:
9 sk
3 5 9 21 25 32 48 89 93 0
4 7 11 26 30 41 52 0
8 10 14 28 46 0
16 19 22 29 47 0
24 27 33 50 0
38 40 0
42 49 0
54 0
56 0
Skiriasi tik įterpiamas skaičius sk ir rezultatai.
|
|
|
|
|
|
|
Įterpiamas skaičius atsiduria pirmosios eilutės pirmame stulpelyje; padidėja lentelės eilučių skaičius |
|
|
|
Lentelė baigiama pildyti, kai pailgėja pirmoji eilutė |
|
|
64 | Lentelė baigiama pildyti, kai pailgėja antroji eilutė |
|
|
|
Lentelė baigiama pildyti, kai pailgėja šeštoji eilutė |
|
|
|
Lentelė baigiama pildyti, kai pailgėja trečioji eilutė |
|
|
|
Padidėja lentelės eilučių skaičius |
Rezultatai
|
|
|
| 1 5 9 21 25 32 48 89 93
3 7 11 26 30 41 52 4 10 14 28 46 8 19 22 29 47 16 27 33 50 24 40 38 49 42 54 56 |
3 5 9 21 25 32 48 89 93 95
4 7 11 26 30 41 52 8 10 14 28 46 16 19 22 29 47 24 27 33 50 38 40 42 49 54 56 |
|
|
|
| 3 5 9 21 25 32 48 64 93
4 7 11 26 30 41 52 89 8 10 14 28 46 16 19 22 29 47 24 27 33 50 38 40 42 49 54 56 |
3 5 9 21 25 31 48 89 93
4 7 11 26 30 32 52 8 10 14 28 41 16 19 22 29 46 24 27 33 47 38 40 50 42 49 54 56 |
|
|
|
| 3 5 9 21 25 32 34 89 93
4 7 11 26 30 41 48 8 10 14 28 46 52 16 19 22 29 47 24 27 33 50 38 40 42 49 54 56 |
3 5 9 13 25 32 48 89 93
4 7 11 21 30 41 52 8 10 14 26 46 16 19 22 28 47 24 27 29 50 33 40 38 49 42 54 56 |