58. KOKIA SKAIČIAVIMO SISTEMA. Pradiniai
duomenys du sveikieji skaičiai a ir s
Parašykite algoritmą, kuris nustatytų, ar egzistuoja tokia skaičiavimo
sistema, kad būtų tenkinama sąlyga
59. PARKETO KLOJIMAS. Stačiakampio kambario grindys klojamos parketo lentelėmis eglutės raštu:
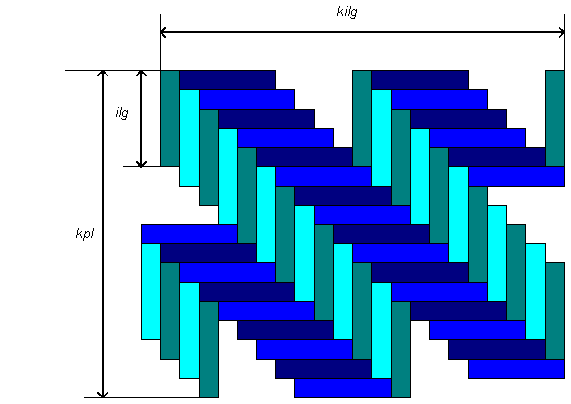
Geriausias lentelių išdėstymas yra toks, kai duoto dydžio lentelėmis (jos nepjaustomos) padengiamas kuo didesnis kambario plotas (aukščiau pateiktame paveiksle lentelių išdėstymas nėra geriausias).
Parašykite algoritmą geriausiam lentelių išdėstymui rasti, t. y. reikia
suskaičiuoti, kiek daugiausiai lentelių galima pakloti duoto ploto kambaryje.
60. TEIGINYS APIE STATŲJĮ TRIKAMPĮ. Stačiojo trikampio statinių a ir b ilgių kvadratų suma yra lygi įžambinės c ilgio kvadratui: a2 + b2 = c2.
Jeigu galima rasti kelis skaičių trejetus, tai reikia rasti trikampio, kurio plotas mažiausias, kraštines. Pavyzdžiui, kai pradiniai duomenys 0, 15, 0, tai kraštinių ilgiai gali būti 9, 15, 12 arba 15, 20, 25, bet rezultatu reikia laikyti sprendinį 9, 15, 12.
61. ATSTATYK SKAIČIUS. Algoritmo parametrai keturi neneigiami skaičiai. Trečiasis skaičius turi būti lygus pirmųjų dviejų sumai, o ketvirtasis pirmųjų dviejų mažiausiam bendrajam kartotiniui. Tačiau ne visi skaičiai žinomi. Vietoj nežinomų skaičių užrašyti nuliai.
Parašykite algoritmą rasti nežinomiems skaičiams, jeigu juos galima rasti. Jeigu galimi keli sprendiniai, tai reikia pateikti mažiausią. (Jei randami keli skaičiai ir galimos kelios jų mažiausios kombinacijos, tai reikia imti tą, kurios pirmesnis skaičius mažesnis).
Jeigu sprendinio negalima rasti, tai reikia palikti nulį nepakeistą.
|
|
|
| 60 90 150 180
60 90 0 0 0 90 0 0 0 0 0 0 0 0 0 180 61 90 0 180 |
60 90 150 180
60 90 150 180 1 90 91 90 1 1 2 1 1 180 181 180 61 90 0 180 |
Reikia atstatyti prarastąjį skaitmenį, jeigu jis tikrai buvo prarastas ir įmanoma tai padaryti (t. y. jei renkant nebuvo padaryta daugiau klaidų). Atkreipiame dėmesį, jog uždavinys gali turėti daugiau negu vieną sprendinį.
Parašykite programą šiam uždaviniui spręsti.
2003 23 2126
2003 123 2126
2003 123 212
2003 123 2126
2003 123 2126
2003 123 2126
3 123 2126
2003 123 2126
3 2123 2126
345 7876 111
SPRENDINIŲ NĖRA
63. PAPRASTOSIOS TRUPMENOS. Reikia rasti
visas teigiamas paprastąsias trupmenas, kurių reikšmė mažesnė už 1. Trupmenos
vardiklis turi neviršyti duotojo natūraliojo
Parašykite programą šiam uždaviniui išspręsti.
|
|
|
|
|
1/2 1/3 1/4 1/5 2/3 2/5 3/5 3/5 4/5 |
Jeigu galimi keli sprendiniai tinka bet kuris. Jeigu uždavinys neturi
nė vieno sprendinio visus keturis skaičius reikia pakeisti nuliais.
|
|
|
| a b dbd mbk | a b dbd mbk |
| 15 20 5 60
15 20 5 120 15 20 0 0 15 20 0 60 0 0 5 60 0 0 20 40 0 0 21 40 0 0 0 0 . . . |
15 20 5 60
0 0 0 0 15 20 5 60 15 20 5 60 15 20 5 60 20 40 20 40 0 0 0 0 1 1 1 1 . . . |
function dbdf (x, y: integer): integer;
begin
if x = 0
then dbdf := y
else dbdf := dbdf(y mod
x, x)
end;
Mažiausiam bendrajam kartotiniui rasti galima pasinaudoti šitokia funkcija:
function mbkf (x, y: integer): integer;
begin
mbkf := x div dbdf(x, y) * y
end;
65. LYGTIS.
anxn + an-1xn-1 + ... + a1x + a0 = 0;
koeficientai an, an-1, ..., a1, a0 yra sveikieji skaičiai.
Parašykite programą visiems
|
|
|
| x3 - 6x2 + 11x - 6 = 0 | 1 2 3 |
| 2x2 + 7x - 4 = 0 | -4 |
| 2x3 + 7x2 - 4x = 0 | -4 0 |
| x2 - 9999x - 10000 = 0 | -1 10000 |
| -x5 + x4 + x3 + x2 + x + 1 = 0 | sveikųjų sprendinių neturi; |
a)
b) galioja lygybė:
anxn + an-1xn-1
+ ... + a1x + a0 = an(x
- x1)(x - x2)...(x -
xn-1)(x - xn);
čia x1, x2, ... xn
lygties šaknys.
Kiekvienai lygčiai skiriama viena pradinių duomenų eilutė. Iš viso pradinių
duomenų byloje yra 8 eilutės. Vadinasi, vienu atlikimu programa turi išspręsti
8 lygtis.
|
|
|
|
| 3 1 -6 11 -6
2 2 7 -4 3 2 7 -4 0 2 1 -9999 -10000 5 -1 1 1 1 1 1 ... |
1 2 3
-4 -4 0 -1 10000 SPRENDINIŲ NĖRA ... |
x3 6x2 + 11x 6 = 0
2x2 + 7x 4 = 0 2x3 + 7x2 4x = 0 x2 9999x 10000 = 0 x5 + x4 + x3 + x2 + x + 1 = 0 ... |
66. DOMINO KAULIUKAI. Duota krūvelė domino
kauliukų. Kiekvienas domino kauliukas perskirtas į dvi puses. Kiekvienoje
pusėje užrašytas skaičius iš intervalo
Reikia nustatyti, ar krūvelėje esančius kauliukus galima išdėlioti į vieną liniją.
Laikykite, kad krūvelė nėra tuščia ir kauliukų skaičius neviršija 20000.
Iš viso pradinių duomenų byloje yra ne daugiau kaip 28 užpildytos eilutės,
nes tiek yra skirtingų kauliukų.
|
|
|
| 0 1 1
1 2 2 2 3 2 |
GALIMA |
67. DAUGIANARIAI. Daugianariu vadinamas tokio pavidalo reiškinys:
anxn + an-1xn-1 + ... + a1x + a0.
Koeficientai an, an-1, ..., a1, a0 yra realieji skaičiai. Laipsniai n, n-1, , 1, 0 sveikieji neneigiami skaičiai. Nariai, kurių ai = 0, praleidžiami. Didžiausias n, kurio an <> 0, vadinamas daugianario laipsniu.
Su daugianariais atliekamos aritmetinės operacijos. Pavyzdžiui,
(-5x3 + 3,5x2 - 1) + (6x3
+ 2x + 1) = (x3 + 3,5x2 + 2x)
(-5x3 + 3x2 - 1) - (-5x3
+ 3x2 - 2) = (1)
(2,5x3 + 1) x (2x2 - 6x)
= (5x5 - 15x4 + 2x2
- 6x)
(5x5 - 15x4 + 2x2
- 6x) / (2x2 - 6x) = (2,5x3
+ 1)
(5x5 - 15x4 + 2x2
- 6x) / (2,5x3 + 1) = (2x2 -
6x)
Pateiktuose pavyzdžiuose daugianariai dalijosi be liekanos (t. y. buvo gaunama liekana, lygi nuliui). Tačiau liekana gali būti nelygi nuliui. Liekanos gavimo operaciją žymėsime simboliu \. Liekanos gavimo operacijos rezultatą apibrėšime šitaip:
Pdalmuo ir Pliekana turi būti tokie, kad būtų tenkinamos sąlygos:
čia Pi daugianaris, d(Pi) daugianario Pi laipsnis.
Pavyzdžiui:
(5x5 - 15x4 + 3x2
- x + 3) / (2,5x3 +1) = (2x2
- 6x);
(5x5 - 15x4 + 3x2
- x + 3) \ (2,5x3 + 1) = (x2
+ 5x + 3).
Parašykite programą, kuri atliktų operacijas +, -, *, / ir \ su daugianariais.
-5x3 + 3,5x2 - 1
vaizduojamas šitaip:
3 -5.0 3.5 0.0 -1.0
|
|
|
| +
3 -5.0 3.5 0.0 -1.0 3 6.0 0.0 2.0 1.0 |
3 1.0 3.5 2.0 0.0
|
68. HAMMINGO SEKA. Reikia generuoti didėjančią natūraliųjų skaičių seką, kurios kiekvienas narys išreiškiamas sandauga
čia i, j, k sveikieji neneigiami skaičiai.
Parašykite programą, kuri generuotų tokią seką. Generavimą reikia baigti, kai gaunamas paskutinis sekos narys, dar neviršijantis 232 1 (t. y. maxlongint) arba paspaudžiamas tarpo klavišas.
Programos dydis neturi viršyti 4Kbaitų.
69. TRUMPIAUSIAS KELIAS. (Šis uždavinys (bei uždavinys Rėmeliai) buvo pasiūlytas Šeštojoje tarptautinėje olimpiadoje, vykusioje 1994 m. Stokholme, Švedijoje, tačiau toje olimpiadoje nebuvo panaudotas.) Duotas stačiakampis laukas, kurio kampų koordinatės yra (0, 0) ir (100, 100). Jo viduje išdėstyta n (n <= 30) kvadratėlių. Reikia rasti trumpiausią kelią iš taško (0, 0) į (100, 100) tokį, kuris nekirstų kvadratėlių.
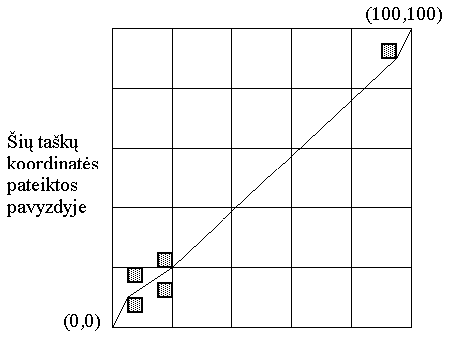
Be to, žinoma, kad
a) kiekvieno kvadratėlio kraštinės ilgis yra 5 vienetai;
b) kvadratėlių kraštinės yra lygiagrečios koordinačių ašims;
c) kvadratėlių kampų koordinatės sveikieji skaičiai;
d) kvadratėliai vienas nuo kito atskirti bent vienu vienetu.
|
|
|
| 5
5 5 5 15 15 10 15 20 90 90 |
0 0
5 10 20 20 95 90 100 100 |
70. RĖMELIAI. Paveikslėlyje vaizduojami
vienas ant kito sudėti rėmeliai. Kiekvienas viršutinis rėmelis dengia apatinius.
Rėmelio plotis 1 simbolis, kiekviena rėmelio briauna ne trumpesnė kaip
3 simboliai. Visų rėmelių matosi bent po vieną kiekvienos briaunos simbolį.
Kampinis simbolis priklauso abiem to kampo briaunoms.
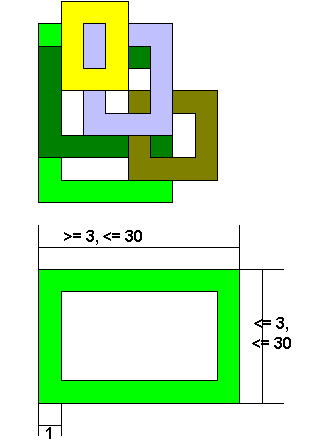
Parašykite programą, kuri surastų, kokia tvarka n (n <=
26) rėmelių yra sudėti vienas ant kito.
Pirmoje bylos eilutėje yra piešinuko aukštis a, antroje piešinuko plotis p. Likusiose a duomenų bylos eilutėse yra piešinukas. Kiekvienos šių eilučių ilgis p. Rėmeliai žymimi skirtingomis lotyniškosios abėcėlės didžiosiomis raidėmis (nuo A iki Z). Fonas žymimas tašku (.).
Pradiniai duomenys tenkina reikalavimus:
a <= 30; p <= 30;
|
|
|
| 9
8 .CCC.... ECBCBB.. DCBCDB.. DCCC.B.. D.B.ABAA D.BBBB.A DDDDAD.A E...AAAA EEEEEE.. |
|