Pirmojo etapo uždavinių sąlygos

71. LAIPSNIAI. Natūralusis skaičius keliamas n-uoju laipsniu, po to nuo jo atskiriama dviženklė galūnė (du skaitmenys). Gautasis dviženklis skaičius vėl keliamas n-uoju laipsniu, vėl imama jo dviženklė galūnė ir t. t. Pavyzdžiui, 123³ = 1860867, 67³ = 300763 ir t.t. Šitaip gauname dviženklių skaičių seką: 67, 63, 47, 23, 67, ...

Parašykite algoritmą dviženklių skaičių sekos periodui rasti (t. y. dviženklių skaičių sekai iki kartojimosi).

72. PINIGAI PAŠTU. Tarkime, kad jūs gavote šitokį laišką:

Dalyvaudamas šiame žaidime laimėsite 15624 litus. Tam laiško pabaigoje parašytu paskutiniuoju (šeštuoju) adresu išsiųskite 1 litą ir šį adresą išbraukite. Savo adresą įrašykite pradžioje, adresus pernumeruokite. Pataisytą laišką perrašykite ir išsiųskite penkiems savo pažįstamiems.

Penki pažįstami, gavę jūsų laiškus, išbrauks paskutinius adresus, o savuosius įrašys pradžioje. Jūsų adresas taps antruoju 5 x 5 = 25 laiškuose. Žaidimas tęsis. Jūsų adresas trečiuoju numeriu bus 25 x 5 = 125 laiškuose, ketvirtuoju – 125 x 5 = 625, penktuoju – 625 x 5 = 3125 ir šeštuoju – 15625 laiškuose. Štai čia jūs ir praturtėsite, gavę 15625 litus. Atėmus žaidimo pradžioje investuotą litą, turėsite 15624 litus pelno.

Tokie ar panašūs laiškai jau yra ne kartą keliavę po pasaulį. Tarkime, pilietis nutarė pradėti žaidimą ir įrašė savo adresą pirmuoju numeriu N₁. Jis susitarė su dar penkiais draugais ir įrašė jų adresus N₂–N₆ numeriais. Praėjus šešiems laiškų rašymo ciklams žaidėjas N₁ tikėjosi gauti 15625 litus, žaidėjas N₂ – 3125 litus, žaidėjas N₃ – 625 litus, N₄ – 125, N₅ – 25 ir N₆ – 5 litus. Iš tikrųjų minėti žaidėjai (visi arba keletas jų) gavo mažiau. Mat ne visi, gavę laiškus, norėjo praturtėti ir įsitraukė į žaidimą.

Nagrinėkime bendresnį atvejį, kai laiškuose rašoma a adresų ir laiškas siunčiamas p žmonių. (Cituoto laiško atveju a = 6, p = 5.)

Parašykite algoritmą, kuris rastų, kiek žmonių, gavusių laiškus, pasitraukė iš žaidimo.

73. LYGIAGRETŪS PROCESAI. (teorinis uždavinys, sprendžiamas be kompiuterio). Yra 100 mokslininkų, kurie labai gerai mintinai skaičiuoja. Kambaryje ant lentos buvo užrašytas nulis. Kiekvienas mokslininkas 100 kartų atliko šiuos veiksmus:

1) įėjo į kambarį;
2) perskaitė ir įsiminė lentoje užrašytą skaičių;
3) išėjo iš kambario;
4) mintinai padidino įsimintą skaičių 37-iais;
5) įėjo į kambarį;
6) nuvalė ant lentos užrašytą skaičių;
7) ant lentos užrašė padidintą skaičių, kurį buvo įsiminęs;
8) išėjo iš kambario.

Didžiausias skaičius, kuris galėjo būti užrašytas lentoje, kai visi mokslininkai baigė vaikščiojimus ir skaičiavimus, yra 370000. Koks yra pats mažiausias skaičius, kuris galėjo būti užrašytas lentoje?

74. KORTŲ KALADĖS. Lošimo kortų kaladėje yra 24 kortos. Jos gali būti išdėstytos bet kokia tvarka. Kortų kaladės perkėlimas – tai kaladės perskyrimas į dvi dalis ir tų dalių sukeitimas vietomis. Kai atliekamas perkėlimo veiksmas, gauname naują kaladę, t. y. kaladę, sudarytą iš tų pačių, tik kitaip išdėstytų kortų.

Turime dvi kortų kalades. Parašykite algoritmą, kuris nustatytų, kiek mažiausiai kartų m reikia perkelti pirmąją kaladę, kad jos kortų išdėstymas sutaptų su antrosios kaladės kortų išdėstymu. Jei kaladės sutampa, tai m = 0. Jei perkėlimo būdu iš pirmosios kaladės negalima gauti antrosios, tai m = –1.

Š – širdys, B – būgnai, K – kryžiai, V – vynai,

ir skaitmeniu, apibūdinančiu kortos akių skaičių

1 – tūzas, 2 – valetas, 3 – dama, 4 – karalius, 9 – devynakė, 0 – dešimtakė.

Pavyzdžiui, Š1 – širdžių tūzas, V3 – vynų dama.

Rezultatas
  0

Staiga stoties administracija sumanė papildyti maršrutą naujomis stotelėmis. Tad vairuotojui teko atspausdinti dar 58 papildomų bilietų komplektus.

1. Ar iš šio duomens galite vienareikšmiškai sužinoti, kiek duotame maršrute buvo stotelių ir kiek atsirado naujų? (Atsakymą pagrįskite.)
2. Išvardykite keletą galimų atsakymų.
3. Kokius reikalavimus turi tenkinti sąlygoje duotas pradinis duomuo, kad atsakymas būtų vienareikšmiškas?

76. SKAIČIŲ BRAUKYMAS. Dažnai žurnalai spausdina skaičių braukymo uždavinius. Jų esmė tokia. Duodama kvadratinė lentelė, užpildyta skaitmenimis, ir seka skaičių, paprastai vienodo ilgio. Reikia rasti šiuos skaičius lentelėje (kad ir kiek kartų jie pasikartotų) ir išbraukti. Braukyti galima horizontaliai, vertikaliai ir įstrižai įvairiomis kryptimis: iš kairės į dešinę, iš dešinės į kairę, iš viršaus į apačią, iš apačios į viršų.

Skaičiai gali persidengti: vieno skaičiaus dalis gali būti kito skaičiaus dalimi. Tikslas: surasti nenubrauktus skaitmenis.

Pirmosios bylos pirmoje eilutėje yra natūralusis skaičius n – lentelės dydis. Po to įrašyta n eilučių, kurių kiekvieną sudaro n skaitmenų, skaitmenys vienas nuo kito atskiriami tarpu.

Antrosios bylos pirmoje eilutėje nurodyti du natūralieji skaičiai: pirmasis reiškia, kiek bus pateikta skaičių, antrasis – keliaženkliai šie skaičiai (ne daugiau kaip dešimt skaitmenų). Tolesnėse eilutėse pateikiami patys skaičiai (po vieną eilutėje), sutvarkyti didėjančia tvarka.

Atkreipiame dėmesį į tai, jog šio uždavinio rezultatas gali būti skaičius, viršijantis maxint. Todėl jį reikėtų aprašyti Paskalio kalbos longint tipu.

long := maxint + int

rezultatas bus neteisingas, nes bus laikoma, kad dešinėje priskyrimo pusėje esantis reiškinys yra integer (o ne longint) tipo. Norint, kad aritmetinės operacijos rezultatas (reiškinys) būtų longint tipo, bent vienas jos operandas turi būti longint tipo.

79. PREKIŲ KONTEINERIAI. Prekybos bazėje yra n konteinerių su maisto produktais. Konteineriai sunumeruoti nuo 1 iki n. Apie kiekvieną konteinerį žinoma tokia informacija: dienų skaičius d, kurioms praėjus produktai turi būti realizuojami už savikainą (t. y. be pelno) ir pelnas, kuris bus gautas, jei produktai bus parduoti iki tos datos. (Produktai pardavinėjami už savikainą nuo (d+1)-osios dienos). Kiekvieną dieną atvežamas į parduotuvę ir realizuojamas tik vienas konteineris.

Kokį didžiausią pelną galima gauti realizavus visus konteinerius ir kokia eilės tvarka reikia juos realizuoti, norint gauti didžiausią pelną?

80.  NEPATIKIMAS RYŠYS. (Šis uždavinys buvo pasiūlytas Septintojoje tarptautinėje olimpiadoje, vykusioje 1995 m. Eindhovene, Olandijoje, tačiau toje olimpiadoje nebuvo panaudotas).  Šis uždavinys – apie pranešimų perdavimą tarp Pranešimų generatoriaus GN ir Vartotojo V. Ryšys yra patikimas, jei Vartotojas gauna tokią pat  pranešimų seką, kokią sugeneravo Generatorius. Kiekvienas pranešimas, kurį išsiunčia Generatorius, turi pasiekti Vartotoją vienintelį kartą ir po baigtinio žingsnių skaičiaus.

Ryšys tarp Generatoriaus ir Vartotojo pavaizduotas tokia diagrama:

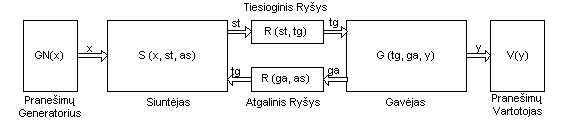
Generatorius generuoja pranešimus ir juos perduoda į išvesties kanalą x. Generatoriaus darbą apibūdina procedūra GN (ji pateikta žemiau). Pranešimas – tai arba 0, arba 1. Pradinę pranešimų seką pažymėkime pi, čia p_i priklauso aibei {0, 1}, o i >= 0.

Siuntėjas S paima pranešimą iš įvesties kanalo x, padaro jo kopiją, perduoda ją tiesioginio ryšio linijomis ir laukia pranešimo iš Gavėjo G. Gautas 1 reiškia, kad pranešimas persiųstas sėkmingai, 0 – kad siunčiant pranešimas buvo sugadintas. Siuntėjas kartos šiuos veiksmus (siųs pranešimą ir lauks patvirtinimo iš Gavėjo) tol, kol negaus 1. Gavęs 1, Siuntėjas paims kitą pranešimą iš įvesties kanalo ir dirbs toliau. Siuntėjo darbą apibūdina procedūra S (visos procedūros pateiktos žemiau).

Perduodant pranešimus ryšio linijomis tarp Siuntėjo ir Gavėjo gali įvykti klaida. Yra žinoma, kad gali būti sugadintas tik baigtinis iš eilės einančių pranešimų skaičius. Kitaip sakant, jei tas pats pranešimas perduodamas daug kartų paeiliui, tai galų gale jis būtinai bus perduotas nesugadintas. Ryšio linijos visuomet nustato, ar perdavimo metu pranešimas buvo sugadintas. Sugadinto pranešimo jos nebesiunčia, o siunčia pranešimą K apie klaidą. Ryšio linijų darbą apibūdina procedūra R.

Gavėjas pasiima pranešimą iš įvesties kanalo. Jei tai yra pranešimas apie klaidą, tai Siuntėjui išsiunčia pranešimą 0 (t. y. prašo pakartotinai išsiųsti pradinį pranešimą). Gavęs nesugadintą pranešimą, pasiunčia jį Vartotojui, Siuntėjui išsiunčia pranešimą 1 ir tęsia darbą toliau. Gavėjo darbą apibūdina procedūra G.

Vartotojas iš įvesties kanalo y pasiima pranešimų seką g_i (i >= 0). Jo darbą apibūdina procedūra V.

Lentelėje (80.1) parodytas vienas iš scenarijų, kaip gali būti perduodama pranešimų seka: p₀ = 0, p₁ = 1. Perduodant pranešimą p₀, įvyko klaida. Stulpeliuose x, st, tg, ga, as, y parodyta, kokie pranešimai laiko momentu T buvo perduodami atitinkamais kanalais.
 

T	x	st	tg	ga	as	y
0	0
1		0
2			K
3				0
4					0
5		0
6			0
7						0
8				1
9					1
10	1
11		1
12			1
13						1

Procedūros, apibūdinančios sistemos darbą

Generatoriaus procedūra:
GN = proc (x!Praneš).
begin i: var Nat & m: var Praneš
| i := 0
; while true
  do m := pi ; x!m
   ; i := i + 1
  od
end

Siuntėjo procedūra:
S = proc (x?Praneš & st!Praneš & as?Praneš).
begin m, a: var Praneš
| x?m
; while true
  do st!m ; as?a
   ; if a = 1 then x?m fi
  od
end

Ryšio linijų procedūra:
R = proc (xx?Praneš & yy!Praneš).
begin m: var Praneš & n: var Nat
| while true
  do n :  Nat
   ; for n do xx?m ; yy!K od
   ; xx?m ; yy!m
  od
end

Gavėjo procedūra:
G = proc (tg?Praneš & ga!Praneš & y!Praneš).
begin m: var Praneš
| while true
  do tg?m
   ; if m = K then ga!0
     else y!m ; ga!1
     fi
  od
end

Vartotojo procedūra:
V = proc (y?Praneš).
begin i: var Nat & m: var Praneš
| i := 0
; while true
  do y?m ; gi := m
   ; i := i + 1
  od
end

A blankas

T	x	st	tg	ga	as	y
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

S = proc (x?Praneš & st!ŽPraneš & as?Praneš).
begin m: var ŽPraneš & a: var Praneš
| m.ž := 0  ; x?m.p
; while true
  do st!m ; as?a
   ; if a = 1
     then m.ž := 1 - m.ž ; x?m.p
     fi
  od
end

G = proc (tg?ŽPraneš & ga!Praneš & y!Praneš).
begin m: var ŽPraneš & u: var Nat
| u := 0
; while true
  do tg?m
   ; if m = K then ga!0
     else if m.ž = u
          then y!m.p ; u := 1 - u
          fi
        ; ga!1
     fi
  od
end

Dabar Siuntėjas prie kiekvieno iš Generatoriaus gauto pranešimo pakaitomis prikabina arba 0, arba 1. Nuo šiol kiekvienas nesugadintas pranešimas (m priklauso ŽPraneš ir m <> K) perduodamas tiesioginio ryšio linijomis, yra pranešimas su atpažinimo ženklu: m.p yra pats pranešimas, o m.ž – jo atpažinimo ženklas.

Procedūroje G atsiranda naujas tarpinis kintamasis u priklauso aibei {0, 1}, kuris rodo, su kokiu atpažinimo ženklu turi ateiti pranešimas iš S. Gavęs pranešimą Gavėjas atlieka tokius veiksmus:

a) jei siunčiant įvyko klaida, tai Siuntėjui išsiunčia 0;
b) jei klaidos neįvyko, bet pranešimo atpažinimo ženklas nesutampa su u reikšme, tai Siuntėjui siunčia 1, bet Vartotojui pranešimo neperduoda;
c) tik tuomet, jei Gavėjas gauna nesugadintą pranešimą su reikiamu atpažinimo ženklu, jis persiunčia pranešimą Vartotojui, pakeičia u reikšmę, pasiunčia 1 Siuntėjui ir ima laukti naujo pranešimo iš Siuntėjo.

Leidžiama keisti tiktai procedūrų S ir G tekstus, esančius tarp simbolių „|“ ir „end“. Draudžiama į šias procedūras įtraukti papildomus kintamuosius, kaip nors keisti likusias procedūras, sudaryti naujas programavimo kalbos konstrukcijas arba keisti įrenginių sujungimo tvarką.

C blankas

S procedūra

S = proc (x?Praneš & st!ŽPraneš & as?Praneš).

begin m: var ŽPraneš & a: var Praneš

...

end

G procedūra

G = proc (tg?ŽPraneš & ga!Praneš & y?Praneš).

begin m: var ŽPraneš & u: var Nat

...

end

Reikia pateikti užpildytus tris atsakymų lapus (A, B ir C blankus).

81. GRAŽIOS LYGTYS.Gražiomis kvadratinėmis lygtimis vadinsime tokias lygtis, kurios tenkina dvi sąlygas:

1) visi jų koeficientai yra sveikieji ir nelygūs nuliui skaičiai;
2) jos turi du sveikuosius ir tarpusavyje nelygius sprendinius.

Eilutėje turi būti penki skaičiai: pirmieji trys – koeficientai a, b, c, toliau – dvi šaknys. Jeigu tokių lygčių duotame intervale nėra, ekrane rašomas tekstas GRAŽIŲ LYGČIŲ NĖRA.

82. GRIOVELIAI. Per kvadratinės plokštelės (82.1 pav.)

centrą lygiagrečiai kraštinėms gali būti išskobtas vienas griovelis

arba du vienas kitam statmeni grioveliai
 

Šiais grioveliais rieda rutuliukas.

Turime n plokštelių su vienu grioveliu, nn plokštelių su dviem grioveliais ir neribotą skaičių plokštelių be griovelių. Iš plokštelių (panaudojus visas n ir nn plokšteles su grioveliais) reikia sudėti tokį mažiausią kvadratą, kad visi grioveliai susisiektų, t. y. jais visais be kliūčių galėtų riedėti rutuliukas. Plokšteles su vienu grioveliu, konstruodami iš jų kvadratą, galime pasukti reikiama kryptimi (taip, kad jų griovelis eitų horizontaliai arba vertikaliai). Rutuliukas gali atsitrenkti tik į tuščią plokštelę.

Parašykite programą šiam uždaviniui išspręsti.

Minuso ženklu (-) žymima plokštelė su vienu grioveliu, kai ji dedama horizontaliai, raide I – plokštelė su vienu grioveliu, kai dedama vertikaliai, pliuso ženklu (+) – su dviem grioveliais, o tuščios plokštelės – nuliu (0).

83. RUBIKO KUBAS. Įsivaizduokite, kad turite Rubiko kubą, sudarytą iš n x n x n mažų kubelių (n <= 30). Po kubą landžioja nykštukas. Būdamas bet kurioje kubo vietoje (bet kuriame mažame kubelyje) jis gali pasiekti bet kurį kitą kubelį. Judėti jam leidžiama lygiagrečiai kuriai nors kubo briaunai. Vienu žingsniu jis gali pereiti tik į kurį nors gretimą kubelį.

Kiekvienas mažas kubelis turi tris koordinates (x, y, z). Koordinatės – natūralieji skaičiai iš intervalo [1, n]. Koordinačių pradžia yra bet kuri Rubiko kubo viršūnė, o x, y, z ašys sutampa su iš tos viršūnės išeinančiomis kubo briaunomis. Kubelio prie tos viršūnės koordinatės yra (1, 1, 1). Paėjus vieną žingsnį kuria nors kryptimi, vienetu padidėja (arba sumažėja) ir atitinkama tos krypties koordinatė.

Per kai kuriuos kubelius negalima pralįsti – jie yra kliūtys, kurias reikia aplenkti. Tokių kliūčių kubelių yra k.

Parašykite programą, kuri rastų trumpiausio kelio nuo kubelio A (x₁, y₁, z₁) iki kubelio B (x₂, y₂, z₂) ilgį, išreikštą žingsnių skaičiumi.

84. DAUGIAKAMPIS. Turime keturių rūšių vienodo ilgio atkarpas:  horizontalias (–), vertikalias (|), pasvirusias 45 laipsnių kampu į dešinę ir į kairę (/), (\). Atkarpas galima kilnoti, bet negalima keisti jų orientacijos.

Reikia nustatyti, ar iš visų turimų atkarpų galima sudėti iškilųjį daugiakampį.

Pastaba. Iracionaliųjų skaičių negalima išreikšti dviejų sveikųjų skaičių santykiu.