Vienuoliktoji moksleivių informatikos olimpiadaPirmojo etapo uždavinių sąlygosJaunesniųjų grupė |
1 (173). NETIKRA MONETA. (teorinis uždavinys). Yra 10 monetų. Žinoma, kad viena iš jų netikra ir yra sunkesnė už kitas monetas. Taip pat turite svirtines svarstykles su dvejomis lėkštelėmis. Jomis galite palyginti lėkštelėse esančių daiktų svorius. Svarstyklių lėkštelėje telpa kelios monetos.
Užduotis. Aprašykite, kaip nustatytumėte, kuri moneta netikra. Svėrimų skaičius turi būti mažiausias.
2 (174). VAIZDO ĮRAŠAI. 240 minučių trukmės vaizdajuostė kainuoja 10 litų 90 centų, 180 minučių trukmės vaizdajuostė kainuoja 9 litus 15 centų. Tomas peržiūrėjo Baltijos televizijos savaitės programą ir panorėjo įsirašyti n laidų. Žinoma kiek valandų ir kiek minučių trunka kiekviena laida. Reikalui esant, bet kuri laida gali būti suskaidyta į dalis ir įrašyta į dvi ar daugiau vaizdajuosčių, o į vieną vaizdajuostę gali būti rašomos kelios laidos. Deja, Tomas neturi nei vienos tuščios vaizdajuostės.
Užduotis. Parašykite algoritmą, kuris suskaičiuotų, kiek mažiausiai pinigų (litų bei centų) reikės išleisti Tomui, norint nusipirkti tiek vaizdajuosčių, kad jų užtektų norimoms laidoms įrašyti.
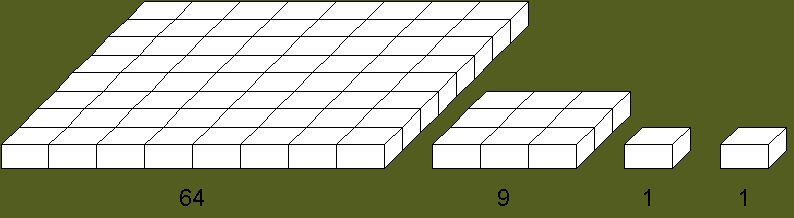
3 (175). PLYTELIŲ DĖLIOJIMAS. Iš n kvadratinių plytelių reikia sudėlioti vienos plytelės storio kvadratų eilę. Pirmiausia sudedamas didžiausias galimas kvadratas. Iš likusių plytelių vėl didžiausias ir t. t.
Užduotis. Parašykite programą, kuri išskaidytų duotą plytelių skaičių į dalis, reikalingas kiekvieno kvadrato statybai. Pavyzdžiui, kai n = 75, tai rezultatas turi būti: 64, 9, 1, 1.
4 (176). NETIKRA MONETA.
a) Yra 10 monetų. Žinoma, kad viena iš jų netikra ir yra sunkesnė už
kitas monetas. Taip pat turite svirtines svarstykles su dvejomis lėkštelėmis.
Jomis galite palyginti lėkštelėse esančių daiktų svorius. Svarstyklių lėkštelėje
telpa kelios monetos. Aprašykite, kaip nustatytumėte, kuri moneta netikra.
Svėrimų skaičius turi būti mažiausias.
b) Duota n (n >= 2) monetų. Parašykite algoritmą, kuris suskaičiuotų, kiek mažiausiai reikia svėrimų, norint nustatyti netikrą monetą uždavinio a) dalyje aprašytomis sąlygomis.
5 (177). GAUKITE SKAIČIŲ. Tarp skaitmenų, užrašytų didėjimo tvarka: 1, 2, 3, 4, 5, 6, 7, 8, 9, reikia įterpti sudėties ir atimties ženklus taip, kad reiškinio reikšmė būtų lygi skaičiui n (n <= maxlongint).
Užduotis. Parašykite programą, sprendžiančią šį uždavinį. Jeigu
galimi keli sprendiniai, reikia spausdinti visus. Jei sprendinių nėra,
turi būti pranešama apie tai.
6 (178). UŽRAŠAS SPIRALE. Parašykite algoritmą,
kuris duotąjį sakinį išspausdintų spirale. Spiralė turi būti atspausdinta
prie kairiojo ekrano krašto. Sakinyje esančius tarpus pakeiskite pliuso
(+) ženklu. Simbolių skaičius sakinyje neviršija 70.
Užduotis. Parašykite programą, kuri suskaičiuotų, kiek dienų (parų), valandų (<24), minučių (<60) ir sekundžių(<60) liko nuo programos paleidimo momento iki trečiojo tūkstantmečio pradžios. Sekundžių šimtąsias dalis ignoruokite. Sekundę, kurią paleidžiama programa, laikykite jau praėjusia.
Trečiasis tūkstantmetis prasidės 2001 m. sausio 1 d. 0 val. 0 min. 0 sek. Laikykite, kad programą vertinimo komisija paleis 2000-aisiais metais.
Pastaba. Duotą momentą Turbo Paskalyje nusako Dos modulio procedūros
GetDate (var Metai, Mėnuo, Diena, Savdiena: word);
GetTime (var Val, Min, Sek, Sek100: word).
8 (180). SLAPTARAŠTIS. Kompiuteris tinka
slaptaraščiams užšifruoti ir iššifruoti. Aprašysime vieną šifravimo būdą.
Parenkamas žodis, vadinamas
raktu. Teksto, kurį reikia užšifruoti,
simboliai suskirstomi į grupes. Simbolių kiekis grupėje sutampa su duoto
rakto ilgiu. Paskutiniojoje grupėje gali būti mažiau raidžių. Pavyzdžiui,
duotas raktas mitas ir tekstas
Sunku pranašauti kaip ateityje
atrodys elektroninės knygos.
|
|
|
|
|
|
| 3 | 2 | 5 | 1 | 4 |
| S | u | n | k | u |
| x | p | r | a | n |
| a | š | a | u | t |
| i | x | k | a | i |
| p | x | a | t | e |
| i | t | y | j | e |
| x | a | t | r | o |
| d | y | s | x | e |
| l | e | k | t | r |
| o | n | i | n | ė |
| s | x | k | n | y |
| g | o | s | . |
Rakto raidės sunumeruojamos. Mažesnį numerį turi raidė, kuri lotyniškoje
abėcėlėje eina pirmiau.
Tuomet parašome pirmojo stulpelio simbolius, po to antrojo, ir t. t.
Gauname užšifruotą tekstą. Jame tarpai pažymėti x simboliu.
kauatjrxtnn.upšxxtayenxoSxaipixdlosguntieeoerėynrakaytskiks
Užduotis. Parašykite algoritmą duotam tekstui užšifruoti.
9 (181). VARLIŲ KONCERTAS. Varlių koncertas. Kartą vienoje kūdroje gyveno daug varlių, ir ne bet kokių, o dresiruotų. Kiekviena varlė sugebėdavo iššokti iš vandens ir sukvarksėti kas tiksliai jai būdingą laiko periodą. Pavyzdžiui, varlės kvarkimo periodas lygus 5. Tai reiškia, kad jei varlė sukvarksėjo pirmą minutę, antrą kartą ji kvarksės po penkių minučių, t. y. šeštą minutę, trečią kartą vienuoliktą minutę ir t. t.
Užduotis. Patekėjus saulei visos varlės iššoko iš vandens ir
sukvarksėjo. Sudarykite algoritmą, kuris nustatytų, po kiek valandų ir
minučių (<60) įvyks antrasis varlių koncertas, t. y. vienu metu iššoks
iš vandens ir sukvarksės visos kūdroje esančios varlės.
Atkreipiame dėmesį, kad valandų skaičius, po kurio įvyks antrasis koncertas, neviršija maxlongint.
10 (182). SEIFO KODAS. Seifo kodas. Žinoma, kad seifo užrakto kodas yra natūralusis skaičius, kurį sudaro n skaitmenų. Be to, žinomos liekanos:
kodą padalijus iš 5.Deja, daugeliu atvejų šių duomenų nepakanka norint vienareikšmiškai nustatyti seifo kodą.
kodą padalijus iš 7.
kodą padalijus iš 11.
Užduotis. Parašykite algoritmą, kuris suskaičiuotų, kiek skirtingų
skaičių galėtų būti seifo užrakto kodais bei pateiktų mažiausią iš jų.
11 (183). SANDAUGOS ĮSTRIŽAINĖSE. Duota nxn dydžio natūraliųjų skaičių lentelė. Patikrinkite, ar šios lentelės pagrindinių įstrižainių skaičių sandaugos lygios. Jei ne, raskite didžiausią kvadratinę lentelę (pradinės lentelės dalį), tenkinančią šią sąlygą. Jei tokių lentelių gali būti kelios, pateikite bet kurią iš jų.
Pastaba. 1x1 dydžio lentelė taip pat gali būti sprendiniu.
|
duomenys |
|
|
||
|
|
|
|
|
4 x 3 x 3 = 6 x 3 x 2 |
|
|
|
|
||
|
|
|
|
||
|
duomenys |
|
Paaiškinimai | ||||
|
|
|
|
|
1 | 2 | 2 x 1 x 3 = 6 <> 1 = 1 x 1 x 1
2 x 1 = 2 x 1 |
|
|
|
|
|
1 | 2 | |
|
|
|
|
|
|||
12 (184). KVADRATINĖ KOCH SALA. Pirmojo laipsnio kvadratinę Koch salą sudaro kvadratas:

n-ojo laipsnio Kvadratinė Koch sala gaunama:
kiekvieną horizontalią (n-1)ojo laipsnio Koch salos
atkarpą pakeitus laužte
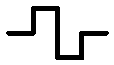 |
O kiekvieną vertikalią atkarpą pakeitus laužte
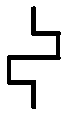 |
Užduotis: Ant popieriaus nubraižykite trečiojo laipsnio Kvadratinę Koch salą. Parašykite algoritmą, kuris pieštų nojo laipsnio Kvadratinę Koch salą. Pradinis duomuo kreivės laipsnis n yra sveikasis skaičius 1<= n<= 8.
13 (185). NAMŲ DAŽYMAS. Statomas modernus daugiaaukštis namas. Jis turės n aukštų. Kiekvienas aukštas gali būti nudažytas viena iš dviejų spalvų: balta arba pilka. Du pilki aukštai negali būti greta, o du balti gali.
Užduotis. Parašykite programą, kuri suskaičiuotų, keliais būdais
galima skirtingai nudažyti n aukštų namą.
|
|
|
|
|
|
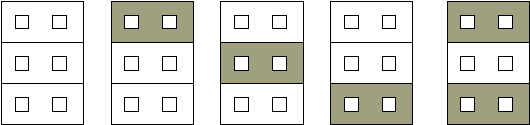
14 (186). KARUSELĖS. Priešingomis kryptimis sukasi dvi karuselės A ir B (žr. pav.). Jos turi a ir b vagonėlių.
Toje pačioje karuselėje negalima pereiti iš vieno vagonėlio į kitą. Tačiau karuselės pastatytos taip arti viena kitos, kad jų sąlyčio vietoje galima peršokti iš vienos karuselės į kitą.
Kiekvienu laiko momentu liečiasi tik po vieną kiekvienos karuselės vagonėlį. Karuselės sukasi tokiu greičiu, kad praėjus vienam laiko momentui liečiasi vagonėliai, gretimi vagonėliams, kurie lietėsi ankstesniu laiko momentu.
Žemiau esančiame paveiksle liečiasi juodai nuspalvinti vagonėliai. Praėjus
vienam laiko momentui liesis pilki vagonėliai.
Pavyzdžiui, karusele A važiuoja keleivis. Jis gali peršokti į karuselės
B vagonėlį ir apsisukus karuselei B vėl grįžti į kažkurį karuselės A vagonėlį.
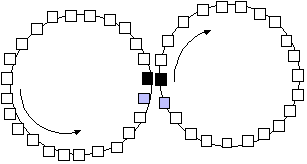
A
B
Užduotis. 1) Žinomi vagonėlių skaičiai abiejose karuselėse a
ir b (20 <= a, b <= maxlongint). Pradiniu
momentu keleivis yra karuselės A vagonėlyje. Reikia suskaičiuoti, keliuose
skirtinguose karuselės A vagonėliuose gali pabuvoti keleivis pasinaudodamas
karusele B.
2) Žinomas karuselės A vagonėlių skaičius a. Reikia rasti, koks
turi būti mažiausias karuselės B vagonėlių skaičius b, kad keleivis
iš bet kurio karuselės A vagonėlio per karuselę B galėtų pakliūti į bet
kurį kitą karuselės A vagonėlį.
Parašykite vieną programą, kuri rastų abu skaičius (t. y. drauge išspręstų
uždavinio pirmą ir antrą dalis).
Skaičius a yra pradinis duomuo abejoms uždavinio dalims, skaičius
b
tik pirmajai daliai.
|
|
|
|
|
23 |
Likusiose n eilučių įrašyta po vieną natūralųjį skaičių, nuo
-n iki n. Tai kvadratėlių viduje esantys skaičiai.
15 (187). BRANGAKMENIAI. Labirintas yra orientuoto medžio pavidalo. Kiekvienoje labirinto aklavietėje paslėpta po vieną tam tikros vertės brangakmenį.
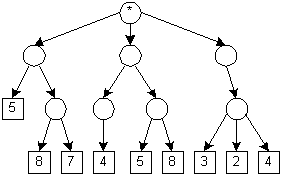
Labirinte galima eiti tik tolyn nuo įėjimo (t. y. rodyklėmis parodytomis
kryptimis). Iš kiekvienos kryžkelės išeina vienas arba daugiau kelių. Į
kiekvieną kryžkelę ir aklavietę veda tik vienas kelias.
Yra tik vienas įėjimas į labirintą.
Paveiksle pateikto labirinto pavyzdyje kryžkelės pažymėtos skrituliukais, aklavietės kvadratėliais, kuriuose įrašyta čia paslėpto brangakmenio vertė. Įėjimas į labirintą pažymėtas žvaigždute.
Berniukas eina į labirintą pasiimti vieno brangakmenio, suprantama, kuo didesnės vertės. Jį lydi labirinto šeimininkas, kuris nori, kad būtų paimtas kuo mažesnės vertės brangakmenis. Berniukas ir šeimininkas susitinka labirinto įėjime. Kiekvienoje kryžkelėje reikia pasirinkti, kuriuo keliu bus keliaujama toliau (aišku, jei yra daugiau kaip vienas kelias). Įėjime renkasi berniukas, kitoje kryžkelėje (į kurią abu pateko po berniuko pasirinkimo) šeimininkas, dar kitoje vėl berniukas ir taip toliau. Ir berniukas ir šeimininkas labai gerai žino labirintą, tad bet kurioje kryžkelėje kiekvienas jų gali pasirinkti, kuriuo labirinto keliu jiems naudingiausia eiti.
Parašykite algoritmą, kuris nustatytų, kokios vertės brangakmenį paims
berniukas, jeigu berniukas ir šeimininkas vaikščios optimaliai.
Toliau byloje įrašyta N+M eilučių. Kiekviena eilutė nusako arba kryžkelę, arba aklavietę. Šios N+M eilučių byloje pateiktos bet kokia tvarka.
Kryžkelę k nusakanti eilutė prasideda raide K. Jei ši kryžkelė
yra labirinto įėjimas, tuomet po raidės K eina nulis (0), jei į ją patenkama
iš kitos kryžkelės, tuomet rašomas pastarosios numeris. Paskutinysis skaičius
eilutėje kryžkelės k numeris.
Kiekviena aklavietę nusakanti eilutė prasideda raide A. Toliau įrašyti
du sveikieji skaičiai: kryžkelės, iš kurios ateinama į šią aklavietę numeris
bei joje esančio brangakmenio vertė v (v sveikasis skaičius,
1 <= v <= maxint).
Pradiniuose duomenyse tarp raidės ir po jos esančio skaičiaus bei tarp
dviejų skaičių palikta po vieną tarpą.
|
|
|
|
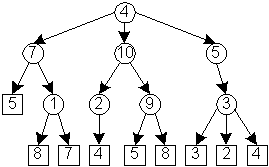
| 8 9
K 10 9 K 4 7 A 9 5 K 5 3 A 3 3 A 1 8 K 0 4 A 2 4 K 4 5 K 4 10 A 1 7 A 3 2 K 7 1 A 3 4 A 9 8 K 10 2 A 7 5 |
|
 |
16 (188). KANDIDATAS Į PREZIDENTUS. Žinomas politinis veikėjas K. Klevas nusprendė kandidatuoti į šalies prezidento postą. Patarėjai kiekvieną dieną skaičiuoja jo reitingą. Deja, situacija keičiasi, vieną dieną buvęs aukštas reitingas kitą dieną krenta ir atvirkščiai.
K. Klevo patarėjai nori pateikti spaudai tokią remiamo kandidato reitingo kitimo suvestinę, kuri nekompromituotų kandidato. Duomenų klastoti negalima, tačiau galima pateikti duomenis tik apie dalį dienų. Sudarant naują dienų (bei reitingų tomis dienomis) sąrašą, dienos turi būti išdėstytos chronologine tvarka, tačiau nebūtina paminėti visas dienas. Atmesti galima bet kurias dienas.
Užduotis. Žinoma, kad reitingas buvo skaičiuojamas d dienų.
Parašykite programą, kuri rastų tokį ilgiausią dienų sąrašą, kad jame reitingai
tiktai didėtų arba bent pasiliktų tokie patys.
Jei sprendinių gali būti keletas, užtenka rasti vieną.
Tolesnėse d eilučių įrašyti atitinkamų dienų reitingai: pirmoje
iš šių eilučių įrašytas reitingas pirmąją skaičiavimo dieną, antroje
antrąją dieną ir t. t. Reitingas yra sveikasis skaičius iš intervalo [-100;
100].
|
|
|
|
| 6
5 10 5 12 8 13 |
4
1 3 5 6 |
Žemiau pateiktas rastasis dienų sąrašas ir reitingai tomis dienomis:
1 diena 3 diena 5 diena 6 diena 5 5 8 13 |
17 (189). MAGIŠKIEJI KVADRATAI. Magiškuoju kvadratu vadiname kvadratinę natūraliųjų skaičių lentelę, kurios kiekvieno stulpelio, kiekvienos eilutės ir abiejų įstrižainių sumos lygios.
Duota nxn kvadratinė natūraliųjų skaičių lentelė. Spėjama, kad ji yra arba galėtų būti magiškasis kvadratas, jei pakeistume kurį nors vieną skaičių.
Užduotis. Parašykite programą, kuri nustatytų, ar duotas kvadratas
yra magiškasis, o jei ne nustatytų, ar galima jame pakeitus vieną skaičių
gauti magiškąjį kvadratą.
Pradiniai duomenys tokie, kad bet kurios eilutės, stulpelio ar įstrižainės
suma neviršys maxlongint.
Jei duotoji lentelė yra magiškasis kvadratas, tai rezultatas turi būti pranešimas: MAGIŠKASIS KVADRATAS.
Jei įmanoma pakeitus vieną skaičių gauti magiškąjį kvadratą, tuomet
pirmoje bylos eilutėje įrašomas pranešimas: GALIMA GAUTI MAGIŠKĄJĮ
KVADRATĄ.
Antroje eilutėje įrašomos keičiamo skaičiaus koordinatės (pirma eilutės,
po to stulpelio numeris) bei skaičius į kurį keičiame.
Jei duotos lentelės neįmanoma vienu pakeitimu paversti magiškuoju kvadratu,
byloje įrašoma: NEĮMANOMA PAKEISTI MAGIŠKUOJU KVADRATU.
|
|
|
| 3
12 17 16 12 15 11 14 13 18 |
GALIMA GAUTI MAGIŠKĄJĮ KVADRATĄ.
2 1 19 |
18 (190). SĄMOKSLININKAI. Žiulio Verno vienos apysakos veikėjai sąmokslininkai norėdami, kad niekas neperskaitytų jų vienas kitam siunčiamų pranešimų, naudojosi šitokiu metodu.
Žinutė paslepiama iš įvairių simbolių (daugiausiai raidžių) sudarytoje
kvadratinėje lentelėje. Iššifravimui naudojamas tokio pat dydžio kvadratinis
tinklelis su skylutėmis tam tikrose vietose. Pavyzdžiui:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|||||
|
|
||||||
|
|
|
|||||
|
|
||||||
|
|
||||||
|
|
|
|||||
|
|
Koduojant pranešimą, žinutės tekstas surašomas į lentelę pagal pasirinktą tinklelį, o likusiuose laisvuose langeliuose įrašomos bet kurios raidės bei simboliai.
Užduotis. Parašykite programą, kuri, turėdama kvadratinę lentelę
su simboliais ir patį pranešimą, surastų šifravimui naudotiną tinklelį.
Pradiniai duomenys tokie, kad sprendinys būtinai egzistuoja. Jei galimi
keli sprendiniai, pakanka pateikti bet kurį vieną.
Antroje eilutėje nurodytas kodavimui naudojamos lentelės kraštinės ilgis N (1 <= N <= 50). Tolesnėse N eilučių pateiktas lentelė. Kiekvienoje eilutėje yra po N simbolių, tarp kurių tarpų nėra.
Lentelėje ir pranešime vartojamos tik didžiosios raidės, skyrybos ženklai,
tarpai. Nei pranešimas, nei jokia lentelės eilutė nesibaigia tarpo simboliu.
|
|
|
| GINKLAI YRA!
7 GUDASAS E MIE ! NYIAGON AAARBDK RNAAAKI ŠLVA!MV !USSO ! |
OXXXXXX
XXXXXXX XXOXXXO XXXXXXX XXXXXOX XOXOXXX XXXXXXX |
19 (191). B. BITAS KURIA TEKSTŲ REDAKTORIŲ.
Programuotojas B.
B. Bitas sugalvojo, kad jam būtų patogu, jei nurodžius fragmentą redaktorius
galėtų suskaičiuoti, kiek kartų tas fragmentas pasikartoja tekste. Be to,
didžiosioms ir mažosioms raidėms skirti taikytų šias taisykles:
Jei paskutinysis teksto eilutės simbolis yra brūkšnys (-), tai reiškia, kad žodis yra keliamas į kitą eilutę. Ieškant fragmento šis brūkšnys ignoruojamas ir skirtingose eilutėse esančios teksto dalys sujungiamos. Jei paskutinysis simbolis nėra brūkšnys, laikoma, kad po paskutiniojo teksto eilutės simbolio eina vienas tarpas.
Pastaba. Tas pats brūkšnys eilutės viduryje reiškia skyrybos ženklą ir tokiu atveju abipus brūkšnio esančių žodžių sujungti nereikia.
Užduotis. Parašykite algoritmą, kuris laikydamasis aukščiau nurodytų
sąlygų, suskaičiuotų kiek kartų duotasis fragmentas sutinkamas tekste.
Antrojoje eilutėje pateiktas teksto eilučių skaičius k (1 <=
k
<= 30). Likusiose k eilučių pateikiamas pats tekstas. Simbolių
skaičius vienoje teksto eilutėje neviršija 80. Tekstas sudarytas iš lietuviškos
abėcėlės didžiųjų ir/arba mažųjų raidžių, tarpų, skyrybos ženklų (taško,
kablelio, brūkšnio, kabliataškio, šauktuko, kabučių ir t.t.), skaitmenų.
|
|
|
| batai
2 Mano ba- taI buvo du. |
|
12 (192). ŽIEMA FANTAZIJOS KARALYSTĖJE. Vieną žiemą Fantazijos karalystėje gausiai pasnigo ir visi keliai tapo nepravažiuojami. Valdžia nusprendė, kad reikia nuvalyti kelius taip, kad iš kiekvieno miesto būtų galima nuvažiuoti į bet kurį kitą, tačiau nebūtinai tiesiogiai. Kad šis darbas būtų padarytas kuo greičiau ir pigiau, nutarta kelius valyti taip, kad nuvalytų kelių bendras ilgis būtų mažiausias.
Žemiau pateiktas Fantazijos karalystės žemėlapio pavyzdys. Miestai žymimi
apskritimu apvestais numeriais. Kelio ilgį nurodo skaičius, parašytas ties
atitinkama atkarpa.
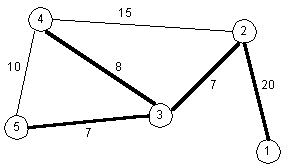 |
| 1 pav. Fantazijos karalystės žemėlapis Keliai, kuriuos reikia nuvalyti, pažymėti storomis linijomis. Nuvalytų kelių ilgis mažiausias. |
Užduotis. Parašykite algoritmą, kuris rastų tokį kelių rinkinį,
kad juos nuvalius iš bet kurio miesto būtų galima patekti į bet kurį kitą,
o bendras nuvalytų kelių ilgis būtų mažiausias. Jei galimi keli sprendimo
variantai, pakanka pateikti bet kurį vieną.
Toliau byloje pateikiama n eilučių, kuriose įrašyta po n tarpais atskirtų teigiamų sveikųjų skaičių: itoje eilutėje surašyti kelių ilgiai nuo iojo miesto iki visų kitų miestų, čia jasis iosios eilutės skaičius reiškia kelio, jungiančio miestus i ir j, ilgį. Jei tarp miestų i ir j nėra tiesioginio kelio, tai kelio ilgis žymimas nuliu.
Nė vienas pradinis duomuo neviršija maxint. Bendras visų kelių ilgis neviršija maxlongint.
Atkreipkite dėmesį, kad jasis skaičius ioje eilutėje
visada sutaps su iuoju skaičiumi joje eilutėje, nes kiekvienu
keliu galima važiuoti į abi puses. Be to, iasis skaičius ioje
eilutėje visada yra 0, nes nėra kelių kilpų.
Likusiose eilutėse nurodykite valomus kelius po vieną į eilutę. Kelias aprašomas dviem skaičiais miestų, kuriuos jungia šis kelias, numeriais.
Valomų kelių pateikimo tvarka nesvarbi. Nurodant konkretų kelią, jį
nusakančių miestų numeriai gali būti pateikiami bet kokia tvarka.
|
|
|
|
| 5
0 20 0 0 0 20 0 7 15 0 0 7 0 8 7 0 15 8 0 10 0 0 7 10 0 |
42
2 1 3 2 5 3 4 3 |
Šiuo atveju uždavinys turi tik vieną sprendinį, tačiau jis gali būti pateiktas nebūtinai taip, kaip parodyta pavyzdyje. Pirmoji eilutė turi būti ta pati, o bet kurios kitos eilutės gali būti sukeistos vietomis ir jose esantys skaičiai taip pat gali būti sukeisti tarpusavyje. |
13 (193). MAŠININIŲ KODŲ INTERPRETATORIUS. Dabar programuotojams beveik nebetenka programuoti mašininiais kodais. Nors iš tikro bet kuri programa (pavyzdžiui, TURBO.EXE) kompiuteriui yra tik kodų, kuriuos galima laikyti (dvejetainiais) skaičių rinkinys. Vieni to rinkinio skaičiai reiškia procesoriaus komandų kodus, kiti duomenis toms komandoms.
Nagrinėsime tokią skaičiavimo mašiną. Mašina turi n laukelių atmintį. Laukeliai sunumeruoti nuo 0 iki n1. Į bet kurį laukelį gali būti įrašytas sveikasis skaičius nuo 0 iki 2k 1. Mašina turi vieną papildomą atminties laukelį, kurį pavadinsime registru R. Į jį galima įrašyti vieną sveikąjį skaičių iš intervalo 0..n1.
Bet kuri šia mašina vykdoma programa įrašoma į atmintį pradedant tam tikru laukeliu (to laukelio numeris vadinamas adresu). Adresas įrašomas į registrą R.
Viena komanda gali užimti 1, 2 arba 3 atminties laukelius. Į žemiau
pateiktą lentelę surašytos visos galimos komandos. I bei J yra sveikieji
skaičiai. Jeigu I ar J reiškia atminties adresą, tuomet I ar J priklauso
intervalui 0..n1, priešingu atveju intervalui 0..2k
1. Brūkšnys langelyje reiškia, kad komanda užima mažiau negu tris laukelius.
Skaičių, esantį atminties laukelyje, kurio adresas X, žymėsime L[X]
| Koman-
dos kodo pirmas laukelis |
Koman-
dos kodo antras laukelis |
Koman-
dos kodo trečias laukelis |
|
|
|
|
|
Į laukelį, kurio adresas I įrašomas skaičius J. |
|
|
|
|
Į laukelį, kurio adresas I, įrašomas skaičius L[J]. Jojo laukelio reikšmė nepasikeičia |
|
|
|
|
Atliekamas veiksmas L[I] + J. Sudėties rezultatas įrašomas į laukelį I (t. y. į laukelį, kurio adresas I) |
|
|
|
|
Atliekamas veiksmas L[I] + L[J]. Sudėties rezultatas įrašomas į laukelį I |
|
|
|
|
Atliekamas veiksmas L[I] J. Atimties rezultatas įrašomas į laukelį I |
|
|
|
|
Atliekamas veiksmas L[I] L[J]. Atimties rezultatas įrašomas į laukelį I. |
|
|
|
|
Skaičius perskaitomas iš klaviatūros, pereinama į naują eilutę ir perskaitytas skaičius įrašomas į laukelį I. |
|
|
|
|
Skaičius L[I] išspausdinamas ekrane ir pereinama į naują eilutę. |
|
|
|
|
Jeigu L[I] > L[J], tuomet į laukelį I įrašomas 1, priešingu atveju 0. |
|
|
|
|
Jeigu L[I] = L[J], tuomet į laukelį I įrašomas 1, priešingu atveju 0. |
|
|
|
|
Jeigu L[I] < L[J], tuomet į laukelį I įrašomas 1, priešingu atveju 0. |
|
|
|
|
Jeigu L[J] = 0, tuomet pereinama į laukelį I, ir vykdoma ten esanti komanda; priešingu atveju vykdomos toliau esančios komandos |
|
|
|
|
Jeigu L[J] <> 0, tuomet pereinama į laukelį I, ir vykdoma ten esanti komanda; priešingu atveju vykdomos toliau esančios komandos. |
|
|
|
|
Pereinama į laukelį I, ir vykdoma tame laukelyje esanti komanda; |
|
|
|
|
Darbas baigiamas (po šios komandos procesorius sustoja) |
Užduotis. Parašykite algoritmą, kuris įvykdytų aprašytai skaičiavimo
mašinai skirtą programą. Laikykite, kad vykdant aprašytai skaičiavimo mašinai
skirtą programą, jokie tarpiniai bei galutiniai duomenys neišeis iš duotų
rėžių. Taip pat programa neužsiciklins.
Pirmoje bylos PROG.EXC eilutėje įrašyta registro R reikšmė (adresas, nuo kurio prasideda programa) bei sveikasis skaičius m (1 <= m <= n). Likusiose m eilučių įrašyta m skaičių: atminties laukelių nuo 0 iki m1 reikšmės.
Skaičius m rodo kiek pirmųjų atminties laukelių užima programa
bei iš anksto žinomi duomenys. Likusiuose atminties laukeliuose turi būti
įrašyti nuliai ir tie laukeliai gali būti panaudoti programos darbo metu.
|
|
|
|
|
|
|
|
| 10 4 | 0 10
2 7 6 13 7 0 0 1 2 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Programa įrašoma pradedant adresu 0. Pirmoji komanda pakeis 7ojo laukelio
turinį. Ten bus įrašyta 7. Po to bus įvykdyta 13 komanda ir pereita prie
komandos, esančios 7ame laukelyje. Šiame laukelyje yra spausdinimo komanda.
Ją atlikus ekrane bus išspausdintas skaičius 6. Po to vykdoma 9tame laukelyje
esanti komanda. Tai pabaigos komanda: darbas baigtas.
14 (194). KELIAUTOJAS. Andrius nusprendė pėsčiomis pakeliauti po Lietuvą ir aplankyti kaimyninius miestelius. Jų skaičius kartu su miestu, kuriame gyvena Andrius, lygus k. Taigi, Andrius nori aplankyti ne mažiau kaip du ir ne daugiau kaip k miestų. Tyrinėdami maršrutus miestus laikykite taškais, kurie nurodyti Dekarto koordinatėmis. Andrius visų miestų koordinates (xi, yi) žino.
Aplankęs paskutinį miestą Andrius grįš į tą, iš kurio pradėjo kelionę. Tarp dviejų miestų jis visada keliauja tuos miestus jungiančia atkarpa.
Be to, Andrius pageidautų, kad per jokį miestą jam nereikėtų pereiti daugiau negu vieną kartą. Vienintelė išimtis pradinis miestas. Jame Andrius pabuvoja du kartus: išeidamas ir sugrįždamas. Atkreipkite dėmesį, kad eidamas iš vieno miestą į kitą, Andrius gali aplankyti ir trečią miestą, jei pastarojo miesto koordinatės priklauso atkarpai, jungiančiai tuos du miestus.
Andrius dar nėra apsisprendęs, kiek laiko norėtų sugaišti kelionėje.
Užduotis. Parašykite programa, kuri padėtų keliautojui apskaičiuoti jo pasirinktų maršrutų ilgius ir nustatytų, ar parinkti maršrutai tenkina Andriaus pageidavimą nė vieno niesto išskyrus pradinio nepereiti daugiau negu vieną kartą. Taip pat reikia parinkti trumpiausią ir ilgiausią maršrutą iš keliautojo pasiūlytų ir tenkinančių Andriaus pageidavimus.
Jei egzistuoja keletas vienodų ilgių trumpiausių ar ilgiausių maršrutų,
užtenka rasti bet kurį iš jų. Galimas atvejis, kad netiks nė vienas maršrutas.
Pradiniai duomenys įvedami iš klaviatūros. Žinoma, kad miestų skaičiaus k yra iš intervalo 2 <= k <= 15, o miestų koordinatės xi, yi iš intervalo 10000 <= xi, yi <= 10000, i = 0, 1, k. Visi duomenys sveikieji skaičiai.
Įvedamų duomenų korektiškumo tikrinti nereikia. Tas pats miestas maršrute gali būti nurodytas kelis kartus, tačiau ne greta (t. y. nebus siūloma keliauti iš to paties miesto į tą patį).
Spausdinamo kelio ilgį reikia apvalinti iki dviejų skaitmenų po kablelio.
| Sveiki!
Kiek daugiausia skirtingų miestų gali įeiti į maršrutą? > 5 Įveskite šių miestų koordinates (x, y): 1 miestas> 1 2 2 miestas> 3 1 3 miestas> 4 2 4 miestas> 5 4 5 miestas> 3 6 Ačiū. Įveskite jūsų pasirinktus maršrutus. Įveskite miestų numerius ta tvarka, kuria norite juos aplankyti. Maršruto pabaigą žymėkite 0. > 1 2 3 4 5 0 Ačiū. Kelio ilgis 13.19 km. Maršrutas geras. Dar bandysite? (t/n) > t Įveskite miestų numerius ta tvarka, kuria norite juos aplankyti. Maršruto pabaigą žymėkite 0. > 1 2 3 4 3 0 Ačiū. Kelio ilgis 11.12 km. Maršrutas netinkamas. Dar bandysite? (t/n) > n Siūlytume tokius maršrutus: trumpiausią - 1 2 3 4 5 (ilgis 13.19 km); ilgiausią 1 2 3 4 5 (ilgis 13.19 km). Laimingo kelio! |
15 (195). PASKALIO PROGRAMŲ PAKAVIMAS. (Vykdymo laikas iki 10 sek.; CPU P133 MHz) Yra sukurta nemažai pakavimo (duomenų glaudinimo) programų. Tačiau kartais galima pasiekti geresnių rezultatų, kai žinoma kaip atrodys pakuojama byla.
Duota byla (prievardis .PAS), kurioje pateikta programa (arba biblioteka) parašyta Turbo Paskalio kalba. Nė viena bylos eilutė nesibaigia tarpo simboliu.
Užduotis. Parašykite dvi programas: 1) duotai bylai supakuoti; 2) supakuotai bylai išpakuoti. Pakuojant bei išpakuojant didžiosios ir mažosios lotyniškos raidės laikomos ekvivalenčiomis. Duotoji bei išpakuotoji bylos visais kitais atžvilgiais privalo sutapti.
Programose draudžiama naudotis bet kuriomis standartinėmis pakavimo
programomis (arj, pkzip, rar ir pan.). Be to išpakuojant
draudžiama vartoti pradinių duomenų bylą (PROGR.PAS), kurioje yra nesuspausta
programa.
Pradiniai duomenys programa, kurią reikia supakuoti įrašyta byloje PROGR.PAS. Bylos dydis neviršija 65000 baitų.
Rezultatą supakuotą programą įrašykite į bylą PROGR.PAK.
Pradiniai duomenys programa, kurią reikia išpakuoti, įrašyta byloje PROGR.PAK. Tai byla, kurią sukūrė Jūsų pakavimo programa.
Rezultatą išpakuotą programą įrašykite į bylą PROGR.KAP.
16 (196). LYGIAGRETŪS SKAIČIAVIMAI. Viena iš galimybių pagreitinti skaičiavimus yra atlikinėti juos lygiagrečiai, tai reiškia, kad kai kurie veiksmai atliekami tuo pačiu laiku. Kai kurie šiuolaikiniai mikroprocesoriai jau turi galimybę lygiagrečiai atlikinėti nepriklausomas komandas. Norint pasinaudoti tokiomis mikroprocesorių galimybėmis, turime rašyti programas pritaikytas lygiagretiems skaičiavimams.
Šiame uždavinyje pasinaudokime tokiu paprastu modeliu. Sakykime, procesorius gali naudoti N atminties laukelių, kurie yra sunumeruoti nuo 1 iki N, bei lygiagrečiai gali atlikti neribotą skaičių komandų.
Procesorius gali atlikti tik šias komandas:
| L I J | į Iąjį atminties laukelį patalpina skaičių J; |
| M I J | į Iąjį atminties laukelį patalpina skaičių iš Jojo laukelio; Jojo atminties laukelio reikšmė nesikeičia; |
| A I J | sudeda Itajame laukelyje esantį skaičių su skaičiumi J, rezultatą patalpiną į Iąjį laukelį; |
| S I J | sudeda Itajame laukelyje esantį skaičių su Jajame laukelyje esančiu skaičiumi, rezultatą patalpiną į Iąjį laukelį |
Pritaikant komandų seką lygiagretiems skaičiavimams, komandos suskirstomos į blokus taip, kad blokuose esančių komandų veiksmai nesikirstų. Taigi visas vienam blokui priklausančias komandas galima atlikti lygiagrečiai.
Atminties laukelių turinys atlikus pradinę veiksmų seką privalo sutapti su atminties laukelių turiniu atlikus tą pačią seką pritaikytą lygiagrečiam skaičiavimui. Jei tą pačią komandą galima paskirti į kelis skirtingus blokus, ją reikia įtraukti į bloką su mažiausiu numeriu.
Užduotis. Parašykite programą, kuri duotąją veiksmų seką pritaikytų lygiagretiems skaičiavimams, t. y. pateiktas komandas suskirstytų į blokus.
Blokų skaičius turi būti kuo mažesnis.
Pirma pateikite pirmąjąm blokui priklausančių komandų sąrašą, po to antrąjąm ir t. t.
Komandų, priklausančių tam pačiam blokui, numeriai turi būti pateikiami
didėjimo tvarka.
|
|
|
|
| 12 6
L 10 4 L 11 3 M 12 11 L 11 5 S 10 12 L 6 5 |
2 6 0 3 0 4 5 0 |
Pirmu žingsniu atliekami trys veiksmai:
L 10 4 L 11 3 L 6 5 Antru žingsniu atliekamas vienas veiksmas: M 12 11 Trečiu žingsniu atliekami du veiksmai: L 11 5 S 10 12 |
17 (197).GALVOSŪKIS. (Vykdymo laikas 2 min.). Teigiami skaičiai surašyti lentelėje iš n eilučių ir m stulpelių. Du lentelės langeliai vadinami gretimais, jei jie liečiasi kraštinėmis. Trijų gretimų langelių skaičiai sudaro lygybę, jei tarp dviejų gretimų skaičių padėjus sudėties, atimties, daugybos arba dalybos (sveikųjų skaičių dalybos div) ženklą, tarp likusių dviejų galime padėti lygybės ženklą. Pavyzdžiui duota tokia lentelė (n = m = 3). Be lentelėje duotų lygybių dar galėtų būti sudarytos ir kitos lygybės, pvz. 197=12
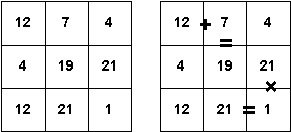
Jei tarp skaičių a ir b padėtas ženklas ž, tuomet
galime nagrinėti reiškinius a ž b bei b ž a.
Užduotis. Parašykite programą, kuri nustatytų kiek daugiausia
lygybių galima suformuoti, jei kiekviename langelyje įrašytas skaičius
gali įeiti tik į vieną lygybę, o pačioje lygybėje gali būti panaudotas
tik vieną kartą. Rezultatas turi būti sudarytų lygybių skaičius.
|
|
|
|
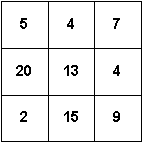
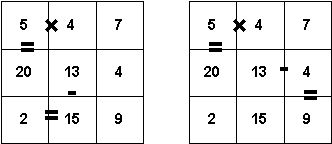
| 3 3
5 4 7 20 13 4 2 15 9 |
|
Vidurinysis skaičius (13), greikalingas sudarant kelias skirtingas lygybes: 2=1513, 13=152, bei 134=9 ir 13=4+9. Tačiau pagal sąlygą, jis gali būti panaudotas tik vieną kartą. |
 |
 |
18 (198). APLINK ŽEMĘ PER 80 DIENŲ. (Vykdymo laikas iki 20 sek.; CPU P133 MHz) Ž. Verno knygoje pasakojama, kaip Filijas Fogas apkeliavo aplink Žemę per 80 dienų. Tačiau gal būt sudarius labai gerą maršrutą, jam būtų pasisekę apkeliauti dar greičiau.
Žinomi įvairių transporto priemonių (traukinių, keltų ir t. t.) tvarkaraščiai. Visomis dienomis tvarkaraščiai yra tokie patys. Apie kiekvieną reisą žinoma šitokia informacija: išvykimo miestas, išvykimo laikas, miestai, kuriuose stojama, kelionės laikas tarp gretimų stočių. Visi tvarkaraščiai nurodyti Grinvičo laiku.
Keliaujama tik į rytus, todėl visą kelionės laiką naudojamasi tik rytų kryptimi vykstančių transporto priemonių tvarkaraščius.
Persėsti iš vienos transporto priemonės į kitą (pvz., iš vieno traukinio į kitą) reikia bent penkių minučių, todėl jei, pavyzdžiui, išlipama stotyje 13:03, tai iš jos išvykti galima anksčiausiai 13:08. Laikoma, kad tarpinėje stotyje transporto priemonės atvyksta ir išvyksta tą pačią minutę.
Užduotis. Žinomas miestas iš kurio pradedama keliauti. Kelionės
pradžia lygiai vidurnaktis Grinvičo laiku. Parašykite programą, kuri nustatytų,
ar galima apkeliauti aplink Žemės rutulį pagal pateiktus susisiekimo priemonių
tvarkaraščius ir, jei galima, praneštų, kada anksčiausiai įmanoma grįžti
namo (t. y. į miestą, iš kurio buvo išvykta).
Kitose eilutėse surašyti reisų tvarkaraščiai. Vienam reisui skirtos kelios eilutės. Pirmoje eilutėje nurodytas išvykimo miesto numeris nr (1 <= nr <= M). Paskui išvykimo laikas: valandos h (0 <= h <= 23) ir minutės min (0 <= min <= 59), tarpinių ir galutinės stočių bendras skaičius ts (1 <= ts <= 150). Kiekvienoje iš tolesnių ts eilučių pateikta informacija apie vieną tarpinę (ar galutinę) stotį: miestas a (1 <= a <= M), į kurį atvykstama, ir kelionės trukmė nuo prieš tai buvusios stoties, t.y. valandos h (0 <= h <= 10000) ir minutės min (0 <= min <= 59).
Taigi, vienam reisui skiriama ts +1 eilutė.
|
duomenys |
|
|
| 5 3 3
3 5 35 3 1 2 44 4 21 7 5 7 18 1 8 23 1 3 16 23 5 6 23 2 3 18 12 2 17 32 |
2 0 46 | Kelionė užtruks 2 paras ir 46 minutes. Iš trečio miesto išvykstama pirmu reisu 5:35 val. ir atvykstama į pirmą miestą po 2 valandų ir 44 minučių, t. y. 8:19 val.. Persėsti į kitą transporto priemonę nespėjama, todėl tenka laukti kito ryto ir 8:23val antru reisu vykstama iki trečio miesto. Kelyje sugaištama 16 valandų ir 23 minutes. Visa kelionė trunka 2 paras ir 46 minutes. |
19 (199). B. BAITAS KURIA TEKSTŲ REDAKTORIŲ. Programuotojas B. Baitas, pasižiūrėjęs į jaunesnįjį kolegą B. Bitą irgi nusprendė sukurti tekstų redaktorių. Viena tekstų redaktoriaus operacijų yra fragmento paieška duotame tekste.
B. Bitas nusprendė, kad jam būtų patogu, jei nurodžius fragmentą redaktorius galėtų surasti visas vietas, kur fragmentas sutinkamas tekste ir sudaryti jų lentelę.
Leidžiami persiklojimai. Pavyzdžiui, fragmentas AMA tekste AMAMA sutinkamas du kartus. Ieškant fragmento būtina atsižvelgti į didžiąsias bei mažąsias raides.
Užduotis. Parašykite algoritmą, kuris surastų visas vietas duotame
tekste kur sutinkamas fragmentas.
Tolesnės n eilučių pateikiamas fragmentas, paskutiniosiose m eilučių tekstas.
Fragmentas bei tekstas sudaryti tik iš lietuviškos abėcėlės simbolių, skaitmenų, tarpų bei skyrybos ženklų. Fragmentas ir tekstas suskaidyti į eilutes po 80 simbolių. Paskutinioji fragmento bei teksto eilutės gali būti trumpesnes. Jokia eilutė nesibaigia tarpo simboliu.
Laikykite, kad po paskutiniojo bet kurios eilutės simbolio eina pirmasis
tolesnės eilutės simbolis. T. y. eilutės pabaiga nereiškia žodžio pabaigos.
Rezultatų byloje eilučių numeriai pateikiami didėjimo tvarka.
|
|
|
| 1 1
batai Mano batai buvo du. |
|
20 (200). ŠAŠKĖS. Kvadratinėje šaškių lentoje ant juodų langelių išdėstytos baltos, juodos šaškės bei viena pilka šaškė. Baltosios ir juodosios šaškės jokių ėjimų nedaro, o pilkoji šaškė kerta juodąsias šaškes pagal įprastas taisykles: kertama įstrižai peršokant kaimyninę šaškę į už jos esantį laisvą juodą langelį ir tokie kirtimo žingsniai tęsiami kol įmanoma. Tačiau yra vienas apribojimas: kertama tik į priekį, t. y. kertančiosios šaškės eilutės numeris gali tik didėti.
Užduotis. Parašykite programą, kuris suskaičiuotų kiek daugiausia
juodų šaškių vienu ėjimu gali nukirsti pilkoji šaškė.
Antroje eilutėje įrašytas bendras šaškių skaičius lentoje.
Toliau yra tiek eilučių kiek lentoje yra šaškių. Kiekviena eilutė nusako
vienos šaškės spalvą ir padėtį šitaip:
S x y
čia S gali būti vienas iš trijų simbolių: J reiškia
juodąją, B baltąją, P pilkąją šaškę; x stulpelio
numeris, y eilutės numeris.
Stulpeliai ir eilutės numeruojami pradedant vienetu iš kairės į dešinę
ir iš apačios į viršų. Langelis (1, 1) yra baltas. Yra lygiai viena ir
tik viena eilutė, prasidedanti raide P (yra viena pilka šaškė).
|
|
|
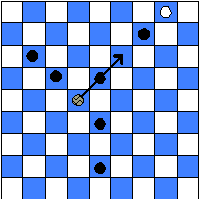 |
| 9
8 J 2 7 J 3 6 B 8 9 J 5 6 P 4 5 J 5 2 J 5 4 J 7 8 |
|
21 (201). MAŠININIŲ KODŲ INTERPRETATORIUS. (Vykdymo laikas iki 50 sek.; CPU P133 MHz) Dabar programuotojams beveik nebetenka programuoti mašininiais kodais. Nors iš tikro bet kuri programa (pavyzdžiui, TURBO.EXE) kompiuteriui yra tik kodų, kuriuos galima laikyti (dvejetainiais) skaičių rinkinys. Vieni to rinkinio skaičiai reiškia procesoriaus komandų kodus, kiti duomenis toms komandoms.
Nagrinėsime tokią skaičiavimo mašiną. Mašina turi n laukelių atmintį. Laukeliai sunumeruoti nuo 0 iki n1. Į bet kurį laukelį gali būti įrašytas sveikasis skaičius nuo 0 iki 2k 1. Mašina turi vieną papildomą atminties laukelį, kurį pavadinsime registru R. Į jį galima įrašyti vieną sveikąjį skaičių iš intervalo 0..n1.
Bet kuri šia mašina vykdoma programa įrašoma į atmintį pradedant tam tikru laukeliu (to laukelio numeris vadinamas adresu). Adresas įrašomas į registrą R.
Viena komanda gali užimti 1, 2 arba 3 atminties laukelius. Į žemiau pateiktą lentelę surašytos visos galimos komandos. I bei J yra sveikieji skaičiai. Jeigu I ar J reiškia atminties adresą, tuomet I ar J priklauso intervalui 0..n1, priešingu atveju intervalui 0..2k 1. Brūkšnys langelyje reiškia, kad komanda užima mažiau negu tris laukelius. Skaičių, esantį atminties laukelyje, kurio adresas X, žymėsime L[X]
Pagal senas tradicijas naudojame 16tainę skaičiavimo sistemą (jos skaitmenys
yra 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F). Ši sistema naudojama
visose (tame tarpe ir įvedimo bei išvedimo) komandose.
| Koman-
dos kodo pirmas laukelis |
Koman-
dos kodo antras laukelis |
Koman-
dos kodo trečias laukelis |
|
|
|
|
|
Į laukelį, kurio adresas I įrašomas skaičius J. |
|
|
|
|
Į laukelį, kurio adresas I, įrašomas skaičius L[J]. Jojo laukelio reikšmė nepasikeičia |
|
|
|
|
Atliekamas veiksmas L[I] + J. Sudėties rezultatas įrašomas į laukelį I (t. y. į laukelį, kurio adresas I) |
|
|
|
|
Atliekamas veiksmas L[I] + L[J]. Sudėties rezultatas įrašomas į laukelį I |
|
|
|
|
Atliekamas veiksmas L[I] J. Atimties rezultatas įrašomas į laukelį I |
|
|
|
|
Atliekamas veiksmas L[I] L[J]. Atimties rezultatas įrašomas į laukelį I. |
|
|
|
|
Skaičius perskaitomas iš klaviatūros, pereinama į naują eilutę ir perskaitytas skaičius įrašomas į laukelį I. |
|
|
|
|
Skaičius L[I] išspausdinamas ekrane ir pereinama į naują eilutę. |
|
|
|
|
Jeigu L[I] > L[J], tuomet į laukelį I įrašomas 1, priešingu atveju 0. |
|
|
|
|
Jeigu L[I] = L[J], tuomet į laukelį I įrašomas 1, priešingu atveju 0. |
|
|
|
|
Jeigu L[I] < L[J], tuomet į laukelį I įrašomas 1, priešingu atveju 0. |
|
|
|
|
Jeigu L[J] = 0, tuomet pereinama į laukelį I, ir vykdoma ten esanti komanda; priešingu atveju vykdomos toliau esančios komandos |
|
|
|
|
Jeigu L[J] <> 0, tuomet pereinama į laukelį I, ir vykdoma ten esanti komanda; priešingu atveju vykdomos toliau esančios komandos. |
|
|
|
|
Pereinama į laukelį I, ir vykdoma tame laukelyje esanti komanda; |
|
|
|
|
Darbas baigiamas (po šios komandos procesorius sustoja) |
Užduotis. Parašykite algoritmą, kuris įvykdytų aprašytai skaičiavimo
mašinai skirtą programą. Laikykite, kad vykdant aprašytai skaičiavimo mašinai
skirtą programą, jokie tarpiniai bei galutiniai duomenys neišeis iš duotų
rėžių. Taip pat programa neužsiciklins.
Pirmoje bylos PROG.EXC eilutėje įrašyta registro R reikšmė (adresas, nuo kurio prasideda programa) bei sveikasis skaičius m (1 <= m <= n). Likusiose m eilučių įrašyta m skaičių: atminties laukelių nuo 0 iki m1 reikšmės.
Skaičius m rodo kiek pirmųjų atminties laukelių užima programa bei iš anksto žinomi duomenys. Likusiuose atminties laukeliuose turi būti įrašyti nuliai ir tie laukeliai gali būti panaudoti programos darbo metu.
Visi byloje PROG.EXC esantys skaičiai užrašyti šešioliktaine sistema.
|
|
|
|
|
|
|
|
| 10 4 | 0 10
2 7 6 D 7 0 0 1 2 E |
|
Pavyzdžio paaiškinimas. Atmintis atrodys taip:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Programa įrašoma pradedant adresu 0. Pirmoji komanda pakeis 7ojo laukelio turinį. Ten bus įrašyta 7. Po to bus įvykdyta D komanda ir pereita prie komandos, esančios 7ame laukelyje. Šiame laukelyje yra spausdinimo komanda. Ją atlikus ekrane bus išspausdintas skaičius 6. Po to vykdoma 9tame laukelyje esanti komanda. Tai pabaigos komanda: darbas baigtas.